Cho tam giác ABC, M là 1 điểm trong tam giác ABC. Đường thẳng AM cắt BC tại D, BM cắt CA tại E, CM cắt AB tại F. CMR nếu \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{0}\) thì M là trọng tâm tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 7 2023
Bài này có nhiều cách làm, vẽ thêm đường phụ cũng được, dùng định lý Menelaus cũng được nhưng lớp 10 thì nên dùng vecto
Ta có:
\(k=\dfrac{AG}{AB}=1-\dfrac{BG}{AB}=1-\dfrac{DE}{AB}=1-\dfrac{2DE}{3EF}\)
Đặt \(\dfrac{AD}{AM}=m\)
\(\Rightarrow\overrightarrow{ED}=m\overrightarrow{EM}+\left(1-m\right)\overrightarrow{EA}\)
\(=m\left(\overrightarrow{EC}+\overrightarrow{CM}\right)+\dfrac{1}{3}\left(m-1\right)\overrightarrow{AC}\)
\(=\dfrac{2}{3}m\overrightarrow{AC}+\dfrac{1}{2}m\overrightarrow{CB}+\dfrac{1}{3}\left(m-1\right)\overrightarrow{AC}\)
\(=\left(m-\dfrac{1}{3}\right)\overrightarrow{AC}+\dfrac{1}{2}m\overrightarrow{CB}\)
Lại có: \(\overrightarrow{EF}=\dfrac{2}{3}\overrightarrow{AB}=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{CB}\)
Mà \(D,E,F\) thẳng hàng nên:
\(\left(m-\dfrac{1}{3}\right)\dfrac{2}{3}=\dfrac{1}{2}m.\dfrac{2}{3}\Leftrightarrow m=\dfrac{2}{3}\)
\(\Rightarrow\overrightarrow{ED}=\dfrac{1}{2}\overrightarrow{EF}\Rightarrow ED=\dfrac{1}{2}EF\)\(\Leftrightarrow\dfrac{DE}{EF}=\dfrac{1}{2}\)
\(\Rightarrow k=\dfrac{2}{3}\)
29 tháng 10 2020
Dựa theo đề bài ta có hình vẽ:
Ta có: MA = 2MB; BN = 5CN => BN = 5/6 BC
Có \(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=-\overrightarrow{BA}+\frac{5}{6}\overrightarrow{BC}\)
Áp dụng định lí menelaus cho tam giác ABN
\(\frac{MA}{MB}.\frac{CB}{CN}.\frac{IN}{IA}=1\)=> \(\frac{2}{1}.\frac{6}{1}.\frac{IN}{IA}=1\Rightarrow IA=12IN\)=> \(\overrightarrow{AI}=\frac{12}{13}\overrightarrow{AN}\)
Ta có: \(\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{AI}=\overrightarrow{BA}+\frac{12}{13}\overrightarrow{AN}=\overrightarrow{BA}+\frac{12}{13}\left(-\overrightarrow{BA}+\frac{5}{6}\overrightarrow{BC}\right)\)rút gọn tính tiếp nhé
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
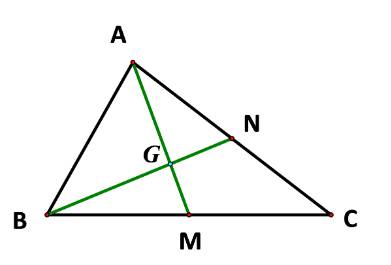
Ta có: \(\overrightarrow {AG} ,\overrightarrow {AM} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AG} } \right| = \frac{2}{3}\left| {\overrightarrow {AM} } \right|\)
Suy ra \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} .\) Vậy \(a = \frac{2}{3}.\)
Ta có: \(\overrightarrow {GN} ,\overrightarrow {GB} \)là hai vecto ngược hướng và \[\left| {\overrightarrow {GN} } \right| = \frac{1}{3}BN = \frac{1}{2}.\left( {\frac{2}{3}BN} \right) = \frac{1}{2}\left| {\overrightarrow {GB} } \right|\]
Suy ra \(\overrightarrow {GN} = - \frac{1}{2}\overrightarrow {GB} .\) Vậy \(b = - \frac{1}{2}.\)