góc xOy vuông góc tai O, điểm A nằm trong góc xOy, B là điểm đối xứng với A qua Õ, C là điểm đối xứng của A qua Oy, gọi D và E lần lượt là giao điểm của AB,AC với OX,Oy
a. Vẽ hình, ghi GT, KL
b. Tứ giác ODAE là hình gì, vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 11 2023
a) Tứ giác OBAC là hình bình hành vì có hai cạnh đối nhau song song (AB và OC) và hai cạnh còn lại cắt nhau vuông góc (OB và AC).
b) Tứ giác ODEF là hình bình hành vì có hai cạnh đối nhau song song (OD và EF) và hai cạnh còn lại cắt nhau vuông góc (OE và DF).
c) Để chứng minh D đối xứng với F qua A, ta cần chứng minh AD = AF và góc DAF = góc FAD.
Vì D là điểm đối xứng của O qua B, nên BD = BO và góc BDO = góc OBD = 90 độ. Tương tự, vì F là điểm đối xứng của O qua C, nên CF = CO và góc CFO = góc OCF = 90 độ.
Do đó, ta có:
- AD = AB + BD = AB + BO = AB + OC = AC + CO = AC + CF = AF
- Góc DAF = góc DAB + góc BAF = góc OBC + góc OCB = 90 độ + 90 độ = 180 độ
Vậy D đối xứng với F qua A.
B2:
a) Ta có:
- M là trung điểm của BC, nên AM song song với DE và AM = DE.
- AD vuông góc với AB và AM vuông góc với BC, nên AD vuông góc với AM.
- Vậy tứ giác ADME là hình chữ nhật vì có hai cạnh đối nhau bằng nhau và các góc vuông.
b) Lấy I đối xứng với D qua M. Ta có:
- IM song song với AD (vì IM và AD đều vuông góc với AB).
- IM = MD (vì I là trung điểm của DM).
- Vậy tứ giác ADIC là hình bình hành vì có hai cạnh đối nhau song song (AD và IC) và hai cạnh còn lại cắt nhau vuông góc (AI và DC).
c) Lấy K đối xứng với E qua M. Ta có:
- KM song song với AE (vì KM và AE đều vuông góc với AC).
- KM = ME (vì K là trung điểm của EM).
- Vậy tứ giác AEKB là hình bình hành vì có hai cạnh đối nhau song song (AE và KB) và hai cạnh còn lại cắt nhau vuông góc (AK và EB).
d) Để chứng minh DK || EI, ta cần chứng minh DK cắt EI vuông góc.
Vì DK là đường chéo của hình chữ nhật ADME, nên DK vuông góc với AM.
Vì EI là đường chéo của hình chữ nhật AEKB, nên EI vuông góc với AK.
Vì AM || AK (vì AM và AK đều song song với BC), nên DK cắt EI vuông góc.
Vậy DK || EI.
19 tháng 9 2021
a: Xét tứ giác OBAC có
\(\widehat{OBA}=\widehat{OCA}=\widehat{BOC}=90^0\)
Do đó: OBAC là hình chữ nhật
29 tháng 11 2023
a) Tứ giác OBAC là hình bình hành vì có hai cạnh đối nhau song song (AB và OC) và hai cạnh còn lại cắt nhau vuông góc (OB và AC).
b) Gọi D là điểm đối xứng với O qua B, E là điểm đối xứng với O qua A, và F là điểm đối xứng với O qua C. Ta có:
- OD = OB (vì D là điểm đối xứng với O qua B).
- OE = OA (vì E là điểm đối xứng với O qua A).
- OF = OC (vì F là điểm đối xứng với O qua C).
Do đó, tứ giác ODEF là hình bình hành vì có hai cạnh đối nhau bằng nhau (OD = OF và OE = OA) và hai cạnh còn lại cắt nhau vuông góc (OE và DF).
c) Để chứng minh D đối xứng với F qua A, ta cần chứng minh AD = AF và góc DAF = góc FAD.
Vì D là điểm đối xứng của O qua B, nên BD = BO và góc BDO = góc OBD = 90 độ. Tương tự, vì F là điểm đối xứng của O qua C, nên CF = CO và góc CFO = góc OCF = 90 độ.
Do đó, ta có:
- AD = AB + BD = AB + BO = AB + OC = AC + CO = AC + CF = AF
- Góc DAF = góc DAB + góc BAF = góc OBC + góc OCB = 90 độ + 90 độ = 180 độ
Vậy D đối xứng với F qua A.
17 tháng 11 2022
a:
| GT | \(\widehat{xOy};A\in\widehat{xOy}\) B đối xứng với A qua Ox,BA cắt Ox tại D C đối xứng với A qua Oy, CA cắt Oy tại E |
| KL | ODAE là hình gì? |
b: A đối xứng với B qua Ox
nên Ox vuông góc với AB tại D
A và C đối xứng với nhau qua Oy
nên Oy vuông góc với AC tại E
Xét tứ giác ODAE có góc ODA=góc OEA=góc EOD=90 độ
nên ODAE là hình chữ nhật
CM
5 tháng 6 2019
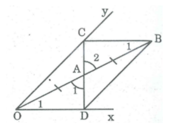
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.
a)
b) Xét tứ giác ODAE có ADO = DOE = OEA = 900
=> tứ giác ODAE là hình chữ nhật