tìm giá trị nghuyên của n để giá trị của biểu thức 3n2-2n+1 chia hết cho giá trị của biểu thức 3n+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) C được xác định <=> x khác +- 2
b) Ta có : \(C=\dfrac{x^3}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-1\right)\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=x-1\)
Để C = 0 thì x - 1 = 0 <=> x = 1 (tm)
c) Để C nhận giá trị dương thì x - 1 > 0 <=> x > 1
Kết hợp với ĐK => Với x > 1 và x khác 2 thì C nhận giá trị dương

\(A=139\)
\(\Leftrightarrow720:\left(x-6\right)=40\)
\(\Leftrightarrow x-6=18\)
hay x=24

Đặt \(A=\frac{9n-4}{2n-7}=\frac{9n-\frac{63}{2}+\frac{33}{2}}{2n-7}=\frac{\frac{9}{2}\left(2n-7\right)+\frac{33}{2}}{2n-7}=\frac{9}{2}+\frac{\frac{55}{2}}{2n-7}\)
Để A có GTLN
\(\Leftrightarrow\frac{\frac{55}{2}}{2n-7}\)có GTLN
\(\Leftrightarrow2n-7\)có GTNN, 2n-7 lớn hơn 0 và n thuộc Z
\(\Leftrightarrow2n-7=1\)
\(\Leftrightarrow2n=8\)
\(\Leftrightarrow n=4\)
Vậy, A có GTLN là 32 khi x=4

P= \(\frac{2n+1}{n+1}\)= \(\frac{2n+2-1}{n+1}\) = \(\frac{2n+2}{n+1}\) - \(\frac{1}{n-1}\) = 2- \(\frac{1}{n-1}\)
a) Vì 2 thuộc Z nên để P thuộc Z thì \(\frac{1}{n-1}\) phải thuộc Z
=> 1 chia hết cho n-1 => n-1 thuộc Ư(1)={1;-1}
TH1:n-1=1 => n=2
TH2:n-1=-1 => n=0. Vậy n thuộc {2;0}
- b) Vì 2 thuộc Z nên để P có GTLN thì -\(\frac{1}{n-1}\) có GTLN => \(\frac{1}{n-1}\) có GTNN
Ta có: 1 thuộc Z và \(\frac{1}{n-1}\) có GTNN => n-1 là số nguyên âm lớn nhất => n-1=-1 => n=0
Khi đó, P= \(\frac{2.0+1}{0+1}\) = \(\frac{1}{1}\)= 1
- Vì 2 thuộc Z nên để P có GTNN thì - \(\frac{1}{n-1}\) có GTNN => \(\frac{1}{n-1}\) có GTLN
=> n-1 là số nguyên dương nhỏ nhất => n-1=1 => n=2
Khi đó, P= \(\frac{2.2+1}{2+1}\)= \(\frac{5}{3}\)
P thuộc Z khi: 2n+1 chia hết cho n+1
<=> 2n+2-1 chia hết cho n+1<=> 2(n+1)-1 chia hết cho n+1
<=> 1 chia hết cho n+1 (vì: 2(n+1) chia hết cho n+1)
<=> n+1 E {-1;1} <=> n E {-2;0}. Vậy: n E {-2;0} P/S: E là thuộc nha!
b)\(P=\frac{2n+1}{n+1}=\frac{2n+2-1}{n+1}=2-\frac{1}{n+1}\)
+)P lớn nhất khi n+1 là số nguyên âm lớn nhất => n+1=-1=>n=-2
Thay vào ta được:
\(P_{max}=2-\frac{1}{-1}=2-\left(-1\right)=3\)
+)P nhỏ nhất khi n+1 là số nguyên dương bé nhất=>n+1=1=>n=0
Thay vào ta được:
\(P_{min}=2-\frac{1}{1}=2-1=1\)

a, ĐKXĐ: \(x\ne1;x\ne-1\)
b, Với \(x\ne1;x\ne-1\)
\(B=\left[\dfrac{x+1}{2\left(x-1\right)}+\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\left[\dfrac{x^2+2x+1+6-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\dfrac{5}{x^2-1}\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =4\)
=> ĐPCM

a) \(A=4,25.\left(58,47+41,53\right)-125=4,25.100-125=425-125=300\)
b) \(4,25.\left(a+41,53\right)-125=53,5\)
\(\Leftrightarrow4,25.\left(a+41,53\right)=178,5\)
\(\Leftrightarrow a+41,53=42\Rightarrow a=0,47\)
ko hiểu hỏi mik nka , t-i-c-k mik nka
Cho biểu thức : A=4,25*(a+41,53)-125a.Tính giá trị của biểu thức A,khi a = 58,47b.Tìm giá trị của a để A =53,5

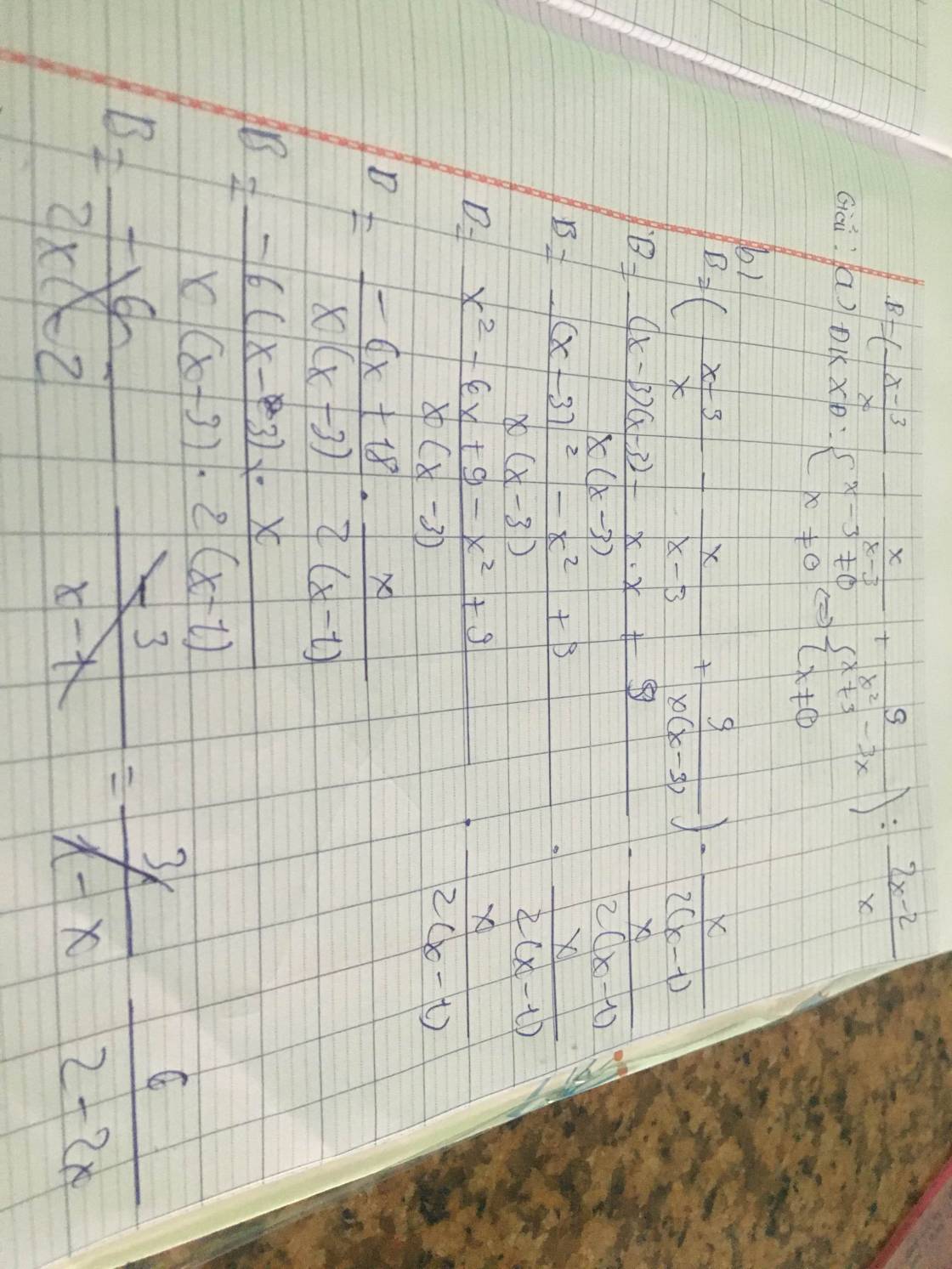 c/
c/
Ta có : B=2=>6/2-2x
<=>6=4-4x
<=>6-4=-4x
<=>-4x=2
<=>x=2/-4=-1/2
d/ĐKXĐ:2-2x≠0
<=>2(1-x)≠0<=>-2(x-1)≠0
<=>x≠1
Để giá trị của biểu thức B nguyên thì 2-2x là Ư(6)
=>2-2x ∈ Ư(6)={±1;±2;±3;±6) Nếu 2-2x=1=> -2x=-1=>x=1/2( thoả mãng)
Rồi còn nhiêu bạn tự xét trường hợp y trang cách làm ở trênn nnhan :;)).À sẽ có mấy cái trường hợp nó giống ĐKXĐ thì bạn ghi trong ngoặc ko thoã mãn nhan.
Ta có:
3n2 - 2n + 1 = (3n + 1)(n - 1) + 2 (sắp phép chia dạng cột)
=> 3n2 - 2n + 1 chia hết cho (3n + 1) khi 3n + 1 € Ư(2) = {-2;-1;1;2}
<=> n = {-1; (-2/3) ; 0 ; 1/3}
Mà n € Z nên n = {-1;0}
Lời giải:
Ta có:
\(3n^2-2n+1=3n^2+n-3n-1+2\)
\(=n(3n+1)-(3n+1)+2=(n-1)(3n+1)+2\)
Để \(3n^2-2n+1\vdots 3n+1\)
\(\Leftrightarrow (n-1)(3n+1)+2\vdots 3n+1\)
\(\Leftrightarrow 2\vdots 3n+1\Rightarrow 3n+1\in \text{Ư}(2)\)
\(\Rightarrow 3n+1\in \left\{\pm 1;\pm 2\right\}\Rightarrow 3n\in \left\{-2; 0; -3; 1\right\}\)
\(\Rightarrow n\in \left\{0;-1\right\}\) do $n$ nguyên.
Vậy............