Cho hàm số \(f\left(x\right)=ã+b\left(a\ne0\right)\)
Hàm số trên đồng biến hay nghịch biến
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Vì $\sqrt{3}-1>0$ nên hàm trên là hàm đồng biến trên $\mathbb{R}$
b.
$F(0)=(\sqrt{3}-1).0+1=1$
$F(\sqrt{3}+1)=(\sqrt{3}-1)(\sqrt{3}+1)+1=(3-1)+1=3$

a, Vì \(a=1>0\) nên đths đồng biến trên R
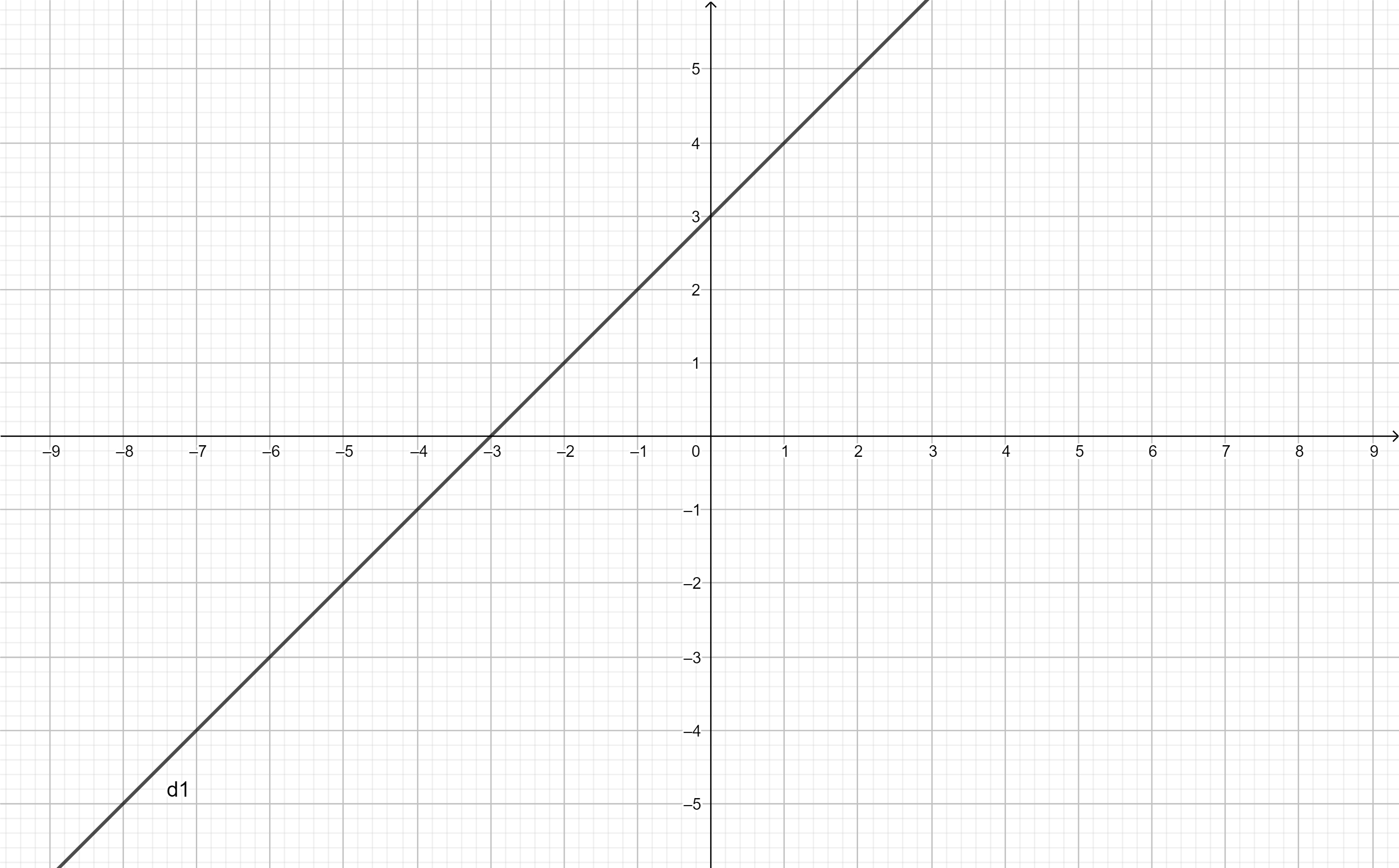
b, Vì (d1)//(d2) nên \(\left\{{}\begin{matrix}a=1\\b\ne3\end{matrix}\right.\)
Vì (d2) cắt trục hoành tại hoành độ 2 nên \(y=0;x=2\)
\(\Leftrightarrow0=2a+b=2+b\Leftrightarrow b=-2\left(tm\right)\)
Vậy đths là \(\left(d_2\right):y=x-2\)

Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)

Do \(\left( { - 2\pi ; - \pi } \right) = \left( { - 2\pi ;\pi - 2\pi } \right)\) nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)

m=2. Khi đó hàm số trở thành: f(x)= -4x-3
Khi đó hàm f(x) luôn nghịch biến vì hệ số a=-4<0

Từ đồ thị hàm số ta thấy khi x tăng từ -3 đến -1 và từ -1 đến 0 thì đồ thị đi lên nên hàm số đồng biến trên các khoảng (-3;-1) và (-1;0).
Khi x tăng từ 0 đến 2 thì đồ thị đi xuống nên hàm số nghịch biến trên (0;2).

a) Hàm số đồng biến khi a > 0
b) Hàm số nghịch biến khi a < 0
Dễ xét 2 Trường hợp là ok :))))
Ta có: \(f\left(x\right)=ã+b\left(a\ne0\right)\left(x\in R\right)\)
TH1: Khi a > 0
* Cho x1 < x2
\(\Leftrightarrow ax_{ }_1< ax_2\)\(\Leftrightarrow ax_1+b< ax_2+b\)
\(\Leftrightarrow f\left(x_1\right)< f\left(x_2\right)\)
TH2: Khi a < 0
* Cho x1 < x2
\(\Leftrightarrow ax_1>ax_2\Leftrightarrow ax_1+b>ax_2+b\)
\(\Leftrightarrow f\left(x_1\right)>f\left(x_2\right)\)
Vậy hàm số trên đồng biến khi a > 0 với mọi \(x\in R\)
Nghịch biến khi a < 0 với mọi \(x\in R\)