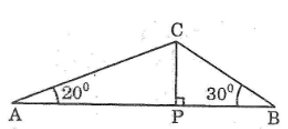
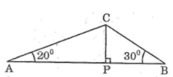
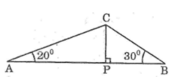
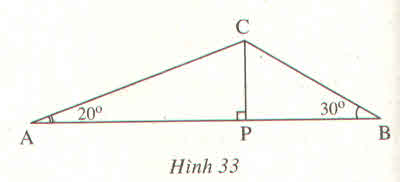
Cho △ABC có các góc A=20o, B=30o, AB=60 cm. Đường cao kẻ từ C đến AB cắt AB tại P. Tính AP, PT, CP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 10 2017
Tính góc A (= 130 độ ). tam giác ACP vuông tại P => AP = cot A .CP (1)
tam giác BCP vuông tại P => BP = cot B . CP (2)
(1) +(2) => AP + BP =cot A .CP +cot B . CP
<=> AB = CP( cot A + cot B)
<=>60= CP ( cot 130 + cot 20 )
=> CP xấp xỉ 31.4
từ đó có thể dễ dàng tính ra AP và BP
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math123ef5cf238a3b88085d95adf94%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%228.5%22%20y%3D%2216%22%3E%26%23x2220%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2216%22%3E20%3C%2Ftext%3E%3Ctext%20font-family%3D%22math138af86134b65d0f10fe33d30dd%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2222.5%22%20y%3D%2216%22%3E%26%23xB0%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2216%22%3E30%3C%2Ftext%3E%3Ctext%20font-family%3D%22math138af86134b65d0f10fe33d30dd%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2222.5%22%20y%3D%2216%22%3E%26%23xB0%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
26 tháng 8 2023
góc ACB=180-20-30=130 độ
Xét ΔABC có
AB/sinC=AC/sinB=BC/sinA
=>BC/sin20=AC/sin30=60/sin130
=>\(BC\simeq26,79\left(cm\right);AC\simeq39,16\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot BA\cdot sinBCA\)
\(=\dfrac{1}{2}\cdot39.16\cdot26.79\cdot sin130=401.83\left(cm^2\right)\)
\(CP=2\cdot\dfrac{S_{ABC}}{AB}=\dfrac{2\cdot401.83}{60}\simeq13,39\left(cm\right)\)
Xét ΔCPA vuông tại P có
tan A=CP/AP
=>13,39/AP=tan20
=>\(AP\simeq36.79\left(cm\right)\)
PB=AB-AP=60-36,79=23,21cm
CM
21 tháng 12 2019
Thay CP = 13,394 vào (1) ta có:
AP = 13,394.cotg 20 ° ≈ 36,801 (cm)
Thay CP = 13,394 vào (2) ta có:
BP = 13,394.cotg 30 ° ≈ 27,526 (cm)
14 tháng 7 2017
Đặt AP=x suy ra BP=60-x.Ta có phương trình
xtg\(20^0\)=(60-x)tg\(30^0\)
Đ/s:AP ≈36,801cm;BP=23,119cm;CP=13,396cm
Tham khảo nha
26 tháng 7 2023
a: Xét ΔBAC vuông tại A có AH là đường cao
nên BA^2=BH*BC
b: BC=căn 18^2+24^2=30cm
CD là phân giác
=>DA/AC=DB/BC
=>DA/4=DB/5=(DA+DB)/(4+5)=18/9=2
=>DA=8cm