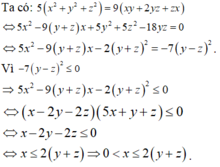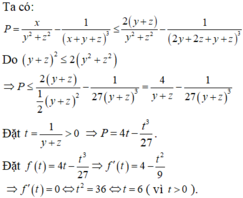Tìm x,y,z biết x3 . 2yz = 2899
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VV
2
VV
1 tháng 1 2020
Có x3.2yz=2899
suy ra 200 bé hơn hoặc bằng 2yz bé hơn 300
suy ra 2899:2yz bé hơn hoặc bằng 2899:200 bé hơn 15
suy ra 2899:2yz lớn hơn 2899:300 lớn hơn 9
Có 9 bé hơn x3 và x3 bé hơn 15 nên x=1
suy ra 13 .2yz=2899
2yz=2899:13
2yz=223
suy ra y=2, z=3
Vậy x=1,y=2,z=3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 7 2023
Bài 3:
a, (\(x\)+y+z)2
=((\(x\)+y) +z)2
= (\(x\) + y)2 + 2(\(x\) + y)z + z2
= \(x^2\) + 2\(xy\) + y2 + 2\(xz\) + 2yz + z2
=\(x^2\) + y2 + z2 + 2\(xy\) + 2\(xz\) + 2yz
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 7 2023
b, (\(x-y\))(\(x^2\) + y2 + z2 - \(xy\) - yz - \(xz\))
= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y3
Đến dây ta thấy xuất hiện \(x^3\) - y3 khác với đề bài, em xem lại đề bài nhé
QT
1
15 tháng 7 2021
Ps : mình nghĩ đề là cm đẳng thức trên nhé
Ta có : \(VT=x\left(y-z\right)-y\left(x+z\right)+z\left(x-y\right)\)
\(=xy-xz-xy-zy+xz-yz=-2yz=VP\)
vậy ta có đpcm
NP
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2021
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2z+1\right)< 1\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-1\right)^2< 1\)
Nếu tồn tại 1 trong 3 số \(x-y;y-z;z-1\) khác 0
Do x; y; z nguyên
\(\Rightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge1\) (vô lý)
\(\Rightarrow x-y=y-z=z-1=0\)
\(\Leftrightarrow x=y=z=1\)
AH
Akai Haruma
Giáo viên
20 tháng 7 2020
Lời giải:
a)
$(x-z)^2+(y-z)^2+y^2+z^2=2xy-2yz+6z-9$
$\Leftrightarrow x^2-2xz+z^2+(y-z)^2+y^2+z^2-2xy+2yz-6z+9=0$
$\Leftrightarrow x^2-2x(z+y)+(z^2+y^2+2yz)+(y-z)^2+(z^2-6z+9)=0$
$\Leftrightarrow x^2-2x(y+z)+(y+z)^2+(y-z)^2+(z-3)^2=0$
$\Leftrightarrow (x-y-z)^2+(y-z)^2+(z-3)^2=0$
Vì $(x-y-z)^2\geq 0; (y-z)^2\geq 0; (z-3)^2\geq 0$ với mọi $x,y,z\in\mathbb{R}$ nên để tổng của chúng bằng $0$ thì:
$(x-y-z)^2=(y-z)^2=(z-3)^2=0$
$\Rightarrow z=3; y=3; x=6$
b)
$x^2+3y^2+z^2+2xy-2yz-2x+4y+10=0$
$\Leftrightarrow (x^2+2xy+y^2)+(y^2-2yz+z^2)+y^2-2x+4y+10=0$
$\Leftrightarrow (x+y)^2+(y-z)^2+y^2-2(x+y)+6y+10=0$
$\Leftrightarrow (x+y)^2-2(x+y)+1+(y-z)^2+(y^2+6y+9)=0$
$\Leftrightarrow (x+y-1)^2+(y-z)^2+(y+3)^2=0$ (lập luận tương tự phần a)
$\Leftrightarrow y=z=-3; x=4$