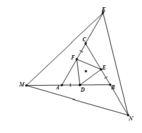
Cho tam giác ABC đều cạnh a (a>0).
1) D là điểm nằm trong tam giác. Gọi M, N, P lần lượt là hình chiếu vuông góc của D trên cạnh BC, CA, AB. Gọi G và G' lần lượt là trọng tâm các tam giác MNP, ABC. Chứng minh rằng D, G, G' thẳng hàng.
2) Tìm GTNN của biểu thức \(y=3\left|\overrightarrow{IA}+\overrightarrow{IB}-\overrightarrow{IC}\right|+\left|\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right|\)theo a khi I thay đổi trên đường thẳng AB.