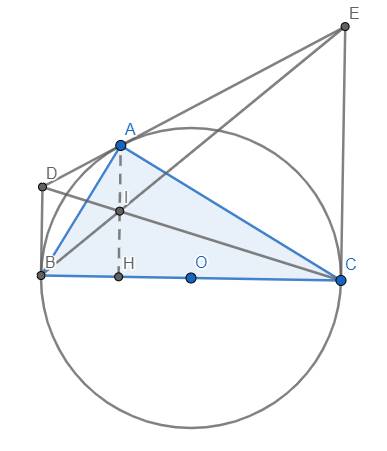
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC vuông tại A với đường cao AH. Các tiếp tuyến với đường tròn (O) tại A và B cắt nhau tại M, CM cắt AH tại I, OM cắt AH tại J.
a, Chứng minh I là trung điểm của AH
b, Cho BC=2R, OM=x. Tính giá trị lớn nhất của AH khi x thay đổi

a,Gọi K là giao điểm của MB và AC.
Theo tính chất 2 tiếp tuyến cắt nhau ta có:
MB=MA
=> góc MAB= góc MBA
Ta có:
góc MAB+góc MAK=90 độ, góc MBA+ góc BKA=90 độ
=> góc MAK= góc MKA
=>MA=MK =>MA=MB=MK
mà tam giác BAK vuông tại A
=> AM là đường trung tuyến của BK
ta có AH vuông góc với BC, KB vuông góc vs BC
=>KB // AH
Áp gụng định lí ta lét ta có:
AI/MK=CI/CM=IH=MB
mà MB=MK=> AI=IH=> I là trung điểm của AH
b,Ta có:
\(AH^2=BH.CH\le\frac{\left(BH+CH\right)^2}{4}=\frac{4R^2}{4}=R^2\Rightarrow AH\le R\)