vẽ đồ thị hàm số y=/2x+2/ và y=/2x/
tìm tọa độ giao điểm cỉa hia đồ thị hàm số đã cho từ đó duy ra phương trình
/2x/=/2x+2/ có 1 nghiệm duy nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 7 2019
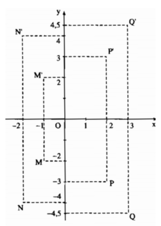
Đồ thị y = -x cắt đồ thị y = x + 1 tại điểm M( x o , y o ). Vì M thuộc cả hai đồ thị nên tọa độ của M phải thỏa mãn các hàm số, nghĩa là:
Đồ thị y = |x| và đồ thị y = |x + 1| chỉ cắt nhau tại một điểm duy nhất M((-1)/2; 1/2).
Suy ra phương trình |x| = |x + 1| chỉ có nghiệm duy nhất x = (-1)/2.
N
30 tháng 11 2021
b. PTHĐGĐ của hai hàm số:
\(x+2=-2x+1\)
\(\Rightarrow x=-\dfrac{1}{3}\)
Thay x vào hs đầu tiên: \(y=-\dfrac{1}{3}+2=\dfrac{5}{3}\)
Tọa độ điểm \(A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)
30 tháng 11 2021
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2020
Pt hoành độ giao điểm:
\(-x^2+2x+3=-2x+1\)
\(\Leftrightarrow x^2-4x-2=0\Rightarrow\left[{}\begin{matrix}x=2+\sqrt{6}\Rightarrow y=-3-2\sqrt{6}\\x=2-\sqrt{6}\Rightarrow y=-3+2\sqrt{6}\end{matrix}\right.\)
Vậy tọa độ giao điểm là: \(\left(2+\sqrt{6};-3-2\sqrt{6}\right)\)
Và \(\left(2-\sqrt{6};-3+2\sqrt{6}\right)\)
T
30 tháng 12 2020
\(\left(P\right):y=-x^2+2x+3\\ \left(d\right):y=-2x+1\)
xét phương trình hoành độ giao điểm của (P) và (d)
\(-x^2+2x+3=-2x+1\)
\(< =>-x^2+4x+2=0\)
\(< =>\left[{}\begin{matrix}x=2+\sqrt{6}\\x=2-\sqrt{6}\end{matrix}\right.\)
thay vào (d) => \(\left[{}\begin{matrix}x=2+\sqrt{6}=>y=-3-2\sqrt{6}\\x=2-\sqrt{6}=>y=-3+2\sqrt{6}\end{matrix}\right.\)
vậy ...
2 tháng 12 2021
\(b,\text{PT hoành độ giao điểm: }x+2=-2x+1\Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\Leftrightarrow y=\dfrac{5}{3}\Leftrightarrow A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\\ c,\text{Gọi }y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne1\\-\dfrac{1}{3}a+b=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{7}{3}\end{matrix}\right.\\ \Leftrightarrow y=2x+\dfrac{7}{3}\)
27 tháng 11 2021
\(b,\text{PT hoành độ giao điểm: }2x=-2x+4\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\)
30 tháng 1 2023
b: Tọa độ giao điểm là:
2x-1=x+2 và y=x+2
=>3x=3 và y=x+2
=>x=1 và y=3
a: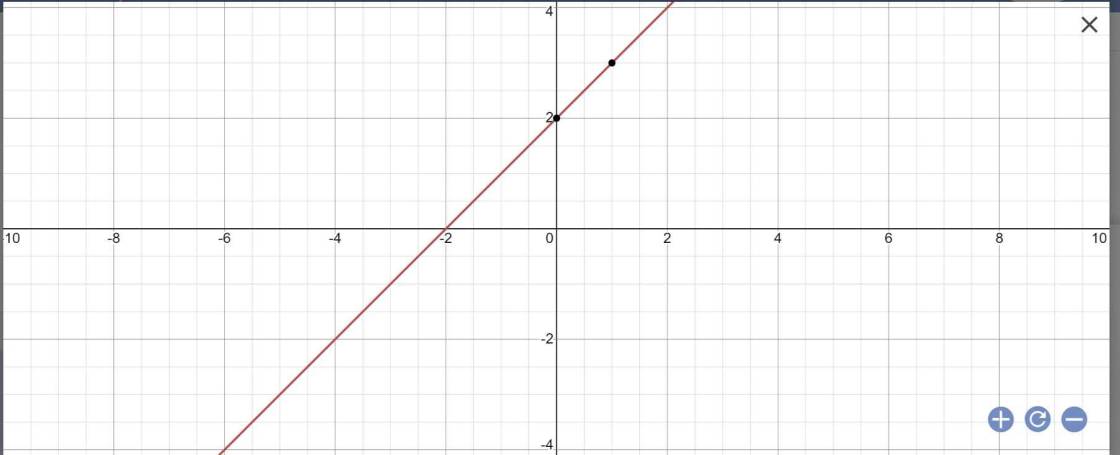 
30 tháng 7 2021
b) Phương trình hoành độ giao điểm của (d) và (d') là:
\(-2x+5=\dfrac{1}{2}x\)
\(\Leftrightarrow-2x-\dfrac{1}{2}x=-5\)
\(\Leftrightarrow x\cdot\dfrac{-5}{2}=-5\)
hay \(x=-5:\dfrac{-5}{2}=-5\cdot\dfrac{2}{-5}=2\)
Thay x=2 vào (d), ta được:
\(y=-2\cdot2+5=-4+5=1\)
HP
7 tháng 4 2021
a, Đồ thị hàm số \(y=3x^2\)
b, Phương trình hoành độ giao điểm của đường thẳng \(y=2x+2\) và parabol \(y=3x^2\) là: \(3x^2=2x+2\Leftrightarrow x=\dfrac{1\pm\sqrt{7}}{3}\)
Với \(x=\dfrac{1+\sqrt{7}}{3}\Rightarrow y=\dfrac{8+2\sqrt{7}}{3}\Rightarrow\left(\dfrac{1+\sqrt{7}}{3};\dfrac{8+2\sqrt{7}}{3}\right)\)
Với \(x=\dfrac{1-\sqrt{7}}{3}\Rightarrow y=\dfrac{8-2\sqrt{7}}{3}\Rightarrow\left(\dfrac{1-\sqrt{7}}{3};\dfrac{8-2\sqrt{7}}{3}\right)\)
7 tháng 4 2021
Sửa đề: \(y=2x+1\)
b) Phương trình hoành độ giao điểm là:
\(3x^2=2x+1\)
\(\Leftrightarrow3x^2-2x-1=0\)
a=3; b=-2; c=-1
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{-1}{3}\)
Thay x=1 vào y=2x+1, ta được:
\(y=2\cdot1+1=3\)
Thay \(x=-\dfrac{1}{3}\) vào y=2x+1, ta được:
\(y=2\cdot\dfrac{-1}{3}+1=\dfrac{-2}{3}+1=\dfrac{1}{3}\)
Vậy: Tọa độ giao điểm là (1;3) và \(\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\)