Rút gọn: \(\sqrt{x-2+2\sqrt{x-3}+}\sqrt{x-3}\) với \(x\ge3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 10 2018
\(\sqrt{x-2+2\sqrt{x-3}}+\sqrt{x-3}=\sqrt{x-3+2\sqrt{x-3}+1}+\sqrt{x-3}=\sqrt{\left(\sqrt{x-3}-1\right)^2}+\sqrt{x-3}=\left|\sqrt{x-3}-1\right|+\sqrt{x-3}\)
Nếu \(3\le x< 4\) thì \(\left|\sqrt{x-3}-1\right|+\sqrt{x-3}=1-\sqrt{x-3}+\sqrt{x-3}=1\)
Nếu \(x\ge4\) thì \(\left|\sqrt{x-3}-1\right|+\sqrt{x-3}=\sqrt{x-3}-1+\sqrt{x-3}=2\sqrt{x-3}-1\)
KK
10 tháng 10 2018
\(\sqrt{x-2+2\sqrt{x-3}}+\sqrt{x-3}\)
=\(\sqrt{x-3+2\sqrt{x-3}+1}+\sqrt{x-3}\)
=\(\sqrt{\left(x-3+1\right)^2}+\sqrt{x-3}\)
=|x-3+1|+\(\sqrt{x-3}\)
= x-2 + \(\sqrt{x-3}\)
5 tháng 5 2021
Câu 1:
Sửa đề: \(B=\left(\dfrac{x}{x+3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{x+3\sqrt{x}}\right)\)
Ta có: \(B=\left(\dfrac{x}{x+3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{x+3\sqrt{x}}\right)\)
\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}+3\right)}+\dfrac{1}{\sqrt{x}+3}\right):\left(\dfrac{x+3\sqrt{x}-2\left(\sqrt{x}+3\right)+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\right)\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}:\dfrac{x+3\sqrt{x}-2\sqrt{x}-6+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x+\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}=1\)
5 tháng 5 2021
Câu 3:
Ta có: \(Q=\left(\dfrac{a}{a-2\sqrt{a}}+\dfrac{a}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}+1}{a-4\sqrt{a}+4}\)
\(=\left(\dfrac{a}{\sqrt{a}\left(\sqrt{a}-2\right)}+\dfrac{a}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-2\right)^2}\)
\(=\dfrac{a+\sqrt{a}}{\sqrt{a}-2}\cdot\dfrac{\sqrt{a}-2}{\sqrt{a}+1}\cdot\dfrac{\sqrt{a}-2}{1}\)
\(=\sqrt{a}\left(\sqrt{a}-2\right)\)
\(=a-2\sqrt{a}\)
NT
1
8 tháng 6 2017
\(C=\sqrt{\left(x+3\right)+2\sqrt{\left(x+3\right)\left(x-3\right)}+\left(x-3\right)}\)
\(=\sqrt{\sqrt{\left(x+3\right)^2}+2\left(x+3\right)\left(x-3\right)+\sqrt{\left(x-3\right)^2}}\)
\(=\sqrt{\left(\sqrt{x+3}+\sqrt{x-3}\right)^2}\)
\(=\sqrt{x+3}+\sqrt{x-3}\)
11 tháng 8 2021
Ta có: \(\dfrac{\sqrt{x}\left(16-\sqrt{x}\right)}{x-4}+\dfrac{3+2\sqrt{x}}{2-\sqrt{x}}-\dfrac{2-3\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{16\sqrt{x}-x-\left(3+2\sqrt{x}\right)\left(\sqrt{x}+2\right)+\left(3\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{16\sqrt{x}-x-3\sqrt{x}-6-2x-4\sqrt{x}+3x-6\sqrt{x}-2\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\)
14 tháng 8 2023
Sửa đề: \(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}\)
\(=\dfrac{x+3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}\)
\(=\dfrac{9\sqrt{x}-9}{x-9}\)
H
12 tháng 3 2023
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)+\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)-3\sqrt{x}-2}{x-4}\right):\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\\ =\dfrac{x+2\sqrt{x}+x-\sqrt{x}-2\sqrt{x}+2-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\times\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\\ =\dfrac{2x-4\sqrt{x}}{\sqrt{x}-2}\times\dfrac{1}{\sqrt{x}-2}\\ =\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}-2}\times\dfrac{1}{\sqrt{x}-2}=\dfrac{2\sqrt{x}}{\sqrt{x}-2}\)
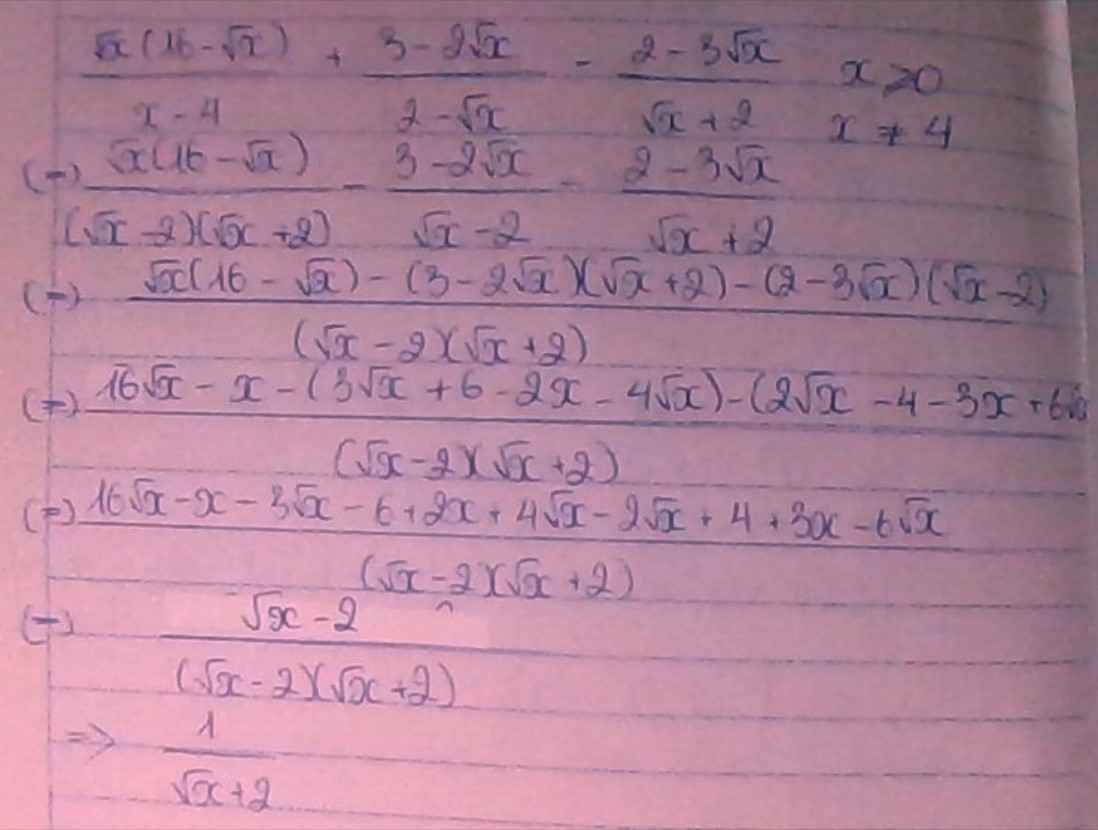
\(\sqrt{x-2+2\sqrt{x-3}}+\sqrt{x-3}\)
\(=\sqrt{x-3+2\sqrt{x-3}+1}+\sqrt{x-3}\)
\(=\sqrt{\left(\sqrt{x-3}+1\right)^2}+\sqrt{x-3}=2\sqrt{x-3}+1\)