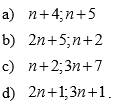bài toán chứng minh 2 số tự nhiên là nguyên tố cùng nhau cả ví dụ nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
uses crt;
var i:integer;
{------------------chuong-trinh-con-kiem-tra-so-nguyen-to----------------------}
function ktnt(x:integer):boolean;
var kt:boolean;
i:integer;
begin
kt:=true;
for i:=2 to x-1 do
if x mod i=0 then kt:=false;
if kt=true then ktnt:=true
else ktnt:=false;
end;
{-------------------------chuong-trinh-chinh----------------------------}
begin
clrscr;
for i:=2 to 9999 do
if (ktnt(i)=true) and (ktnt(i+2)=true) then
begin
writeln(i,',',i+2);
delay(500);
end;
readln;
end.
Bài 4:
uses crt;
var a,b,c,kt:integer;
begin
clrscr;
write('Nhap ngay:'); readln(a);
write('Nhap thang:'); readln(b);
write('Nhap nam:'); readln(c);
kt:=0;
if (b=1) and (0<a) and (a<=31) then kt:=1;
if (b=2) and (0<a) and (a<=28) then kt:=1;
if (b=2) and (0<a) and (a<=29) and (c mod 4=0) then kt:=1;
if (b=3) and (0<a) and (a<=31) then kt:=1;
if (b=4) and (0<a) and (a<=30) then kt:=1;
if (b=5) and (0<a) and (a<=31) then kt:=1;
if (b=6) and (0<a) and (a<=30) then kt:=1;
if (b=7) and (0<a) and (a<=31) then kt:=1;
if (b=8) and (0<a) and (a<=31) then kt:=1;
if (b=9) and (0<a) and (a<=30) then kt:=1;
if (b=10) and (0<a) and (a<=31) then kt:=1;
if (b=11) and (0<a) and (a<=30) then kt:=1;
if (b=12) and (0<a) and (a<=31) then kt:=1;
if kt=0 then writeln('Khong hop le')
else writeln('Hop le');
readln;
end.

uses crt;
var i,n,m,k,d:integer;
{---------------chuong-trinh-con-tim-ucln--------------------}
function ucln(x,y:integer):integer;
var t:integer;
begin
while y<>0 do
begin
t:=x mod y;
x:=y;
y:=t;
end;
ucln:=x;
end;
{------------chuong-trinh-con-kiem-tra-so-nguyen-to-------------------}
function nt(b:longint):boolean;
var j:longint;
begin
nt:=true;
if (b=2) or (b=3) then exit;
nt:=false;
if (b=1) or (b mod 2=0) or (b mod 3=0) then exit;
j:=5;
while j<=trunc(sqrt(b)) do
begin
if (b mod j=0) or (b mod (j+2)=0) then exit;
j:=j+6;
end;
nt:=true;
end;
{---------------chuong-trinh-chinh---------------------}
begin
clrscr;
write('Nhap N: '); readln(N);
write('Nhap M: '); readln(M);
d:=0;
k:=ucln(N,M);
for i:=1 to k do
if nt(i) then d:=d+1;
if d>0 then writeln('2 so nay tuong duong voi nhau')
else writeln('2 so nay khong tuong duong voi nhau');
readln;
end.

1:
a: Gọi d=ƯCLN(n+5;n+4)
=>\(\left\{{}\begin{matrix}n+5⋮d\\n+4⋮d\end{matrix}\right.\)
=>\(n+5-n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>n+4 và n+5 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(2n+5;n+2)
=>\(\left\{{}\begin{matrix}2n+5⋮d\\n+2⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+4⋮d\end{matrix}\right.\)
=>\(2n+5-2n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+5 và n+2 là hai số nguyên tố cùng nhau
c: Gọi d=ƯCLN(3n+7;n+2)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\3n+6⋮d\end{matrix}\right.\)
=>\(3n+7-3n-6⋮d\)
=>\(1⋮d\)
=>d=1
=>3n+7 và n+2 là hai số nguyên tố cùng nhau
d: Gọi d=ƯCLN(2n+1;3n+1)
=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+1⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+2⋮d\end{matrix}\right.\)
=>\(6n+3-6n-2⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+1 và 3n+1 là hai số nguyên tố cùng nhau
a) Gọi d là ƯCLN của n + 4 và n + 5
⇒ n + 4 ⋮ d và n + 5 ⋮ d
⇒ (n + 5 - n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 4 và n + 5 luôn là cặp SNT cùng nhau
b) Gọi d là ƯCLN của 2n + 5 và n + 2
⇒ 2n + 5 ⋮ d và n + 2 ⋮ d
⇒ 2n + 5 ⋮ d và 2(n + 2) ⋮ d
⇒ (2n + 5 - 2n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 5 và n + 2 luôn là cặp SNT cùng nhau
c) Gọi d là ƯCLN của n + 2 và 3n + 7
⇒ n + 2 ⋮ d và 3n + 7 ⋮ d
⇒ 3(n + 2) ⋮ d và 3n + 7 ⋮ d
⇒ (3n + 7 - 3n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 2 và 3n + 7 luôn là cặp SNT cùng nhau
d) Gọi d là ƯCLN của 2n + 1 và 3n + 1
⇒ 2n + 1 ⋮ d và 3n + 1 ⋮ d
⇒ 3(2n + 1) ⋮ d và 2(3n + 1) ⋮ d
⇒ (6n + 3 - 6n - 2) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 1 và 3n + 1 luôn là cặp SNT cùng nhau

1. Nhận xét rằng a là số tự nhiên lẻ và ab + 4 là một số chẵn.
Nếu d là một ước chung của a và ab + 4 ( d > 1), thì do a lẻ nên d phải là số lẻ.
Do ab chia hết cho d nên 4 chia hết cho d, suy ra d \(\in\) { 2; 4 }. (mâu thuẫn)..
b) Gọi d là ước chung lớn nhất của n + 2 và 3n + 11.
Suy ra \(\hept{\begin{cases}n+2⋮d\\3n+11⋮d\end{cases}\Rightarrow\hept{\begin{cases}3n+6⋮d\\3n+11⋮d\end{cases}}}\).
Suy ra \(3n+11-\left(3n+6\right)=5⋮d\).
Vì vậy d = 1 hoặc d = 5.
Để n + 2 và 3n + 11 là hai số nguyên tố cùng nhau thì d = 1.
Nếu giả sử ngược lại \(\hept{\begin{cases}n+2⋮5\\3n+11⋮5\end{cases}}\) \(\Leftrightarrow n+2⋮5\).
Suy ra \(n\) chia 5 dư 3 hay n = 5k + 3.
Vậy để n + 2 và 3n + 11 là hai số nguyên tố cùng nhau, thì n chia cho 5 dư 0, 1, 2, 4 hay n = 5k, n = 5k +1, n = 5k + 2, n = 5k + 4.

1 a chia hết cho b khi a là bội của b
b là ước của a
2 a chia hết cho m, b chia hết cho m
=> (a+b) chia hết cho m
a chia hết cho m, b chia hết cho m, c chia hết cho m
=> (a+b+c) chia hết cho m
3 Dấu hiệu chia hết cho 2 là những số có tận cùng là 0,2,4,6,8
Dấu hiệu chia hết cho 3 là những số có tổng chia hết cho 3
Dấu hiệu chia hết cho 5 là những số có tận cùng là 0 hoặc 5
Dấu hiệu chia hết cho 9 là những số có tổng chia hết cho 9
4 số nguyên tố là số tự nhiên >1, chỉ có 2 ước là 1 và chính nó
VD 47
hợp số là số tự nhiên >1, có nhiều hơn 2 ước.
VD 8
5 2 số nguyên tố cùng nhau là 2 số có ƯCLN bằng 1
VD 2 và 3