Mọi người giúp em giải giúp em với ạ. Cảm ơn nha!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


pt 2CH3COOH+Mg→(CH3COO)2Mg +H2
n(CH3COO)2Mg =1,42/142=0,1 mol
theo pt nCH3COOH =2n(CH3COO)2Mg =0,2 mol
suy ra CM=0,2 /0,5=0.4 mol/l
theo pt nH2 =n(CH3COO)2Mg =0,1 mol
suy ra VH2 =2,24l
KOH+CH3COOH->CH3COOK+H2O
0,2------0,2
=>VKOH=\(\dfrac{0,2}{0,5}\)=0,4l=400ml

10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)

Bài 1:
a: \(=-10x^3+20x^4-5x\)
b: \(=\dfrac{1}{3}a^2b+7a^5-1\)
c: \(=a^3+8+25-a^3=33\)
d: \(=x^2-16+8-x^3=-x^3+x^2-8\)
e: \(=a^3+1+8-a^3=9\)
f: \(=\dfrac{7-2x+4x-8}{2x+3}=\dfrac{2x-1}{2x+3}\)
g: \(=\dfrac{3}{2\left(x+3\right)}-\dfrac{2}{x\left(x+3\right)}\)
\(=\dfrac{3x-4}{2x\left(x+3\right)}\)

1 The meeting was canceled 3 days ago
2 She told me she was watching a film with her sister then
3 I admire the guitarist who is perfroming on the stage
4 Had it not been for Pauline's interest, the project would have been abandoned


Đề dài thế này sao giải thích nhanh cho e đc
Part 1
1 C
2 B
3 D
4 C
5 B
6 A
Part 2
1 T
2 F
3 F
4 F
V
1 That old house has just been bought
2 If he doesn't take these pills, he won't be better
3 I suggest taking a train
4 Spending the weekend in the countryside is very wonderful

-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
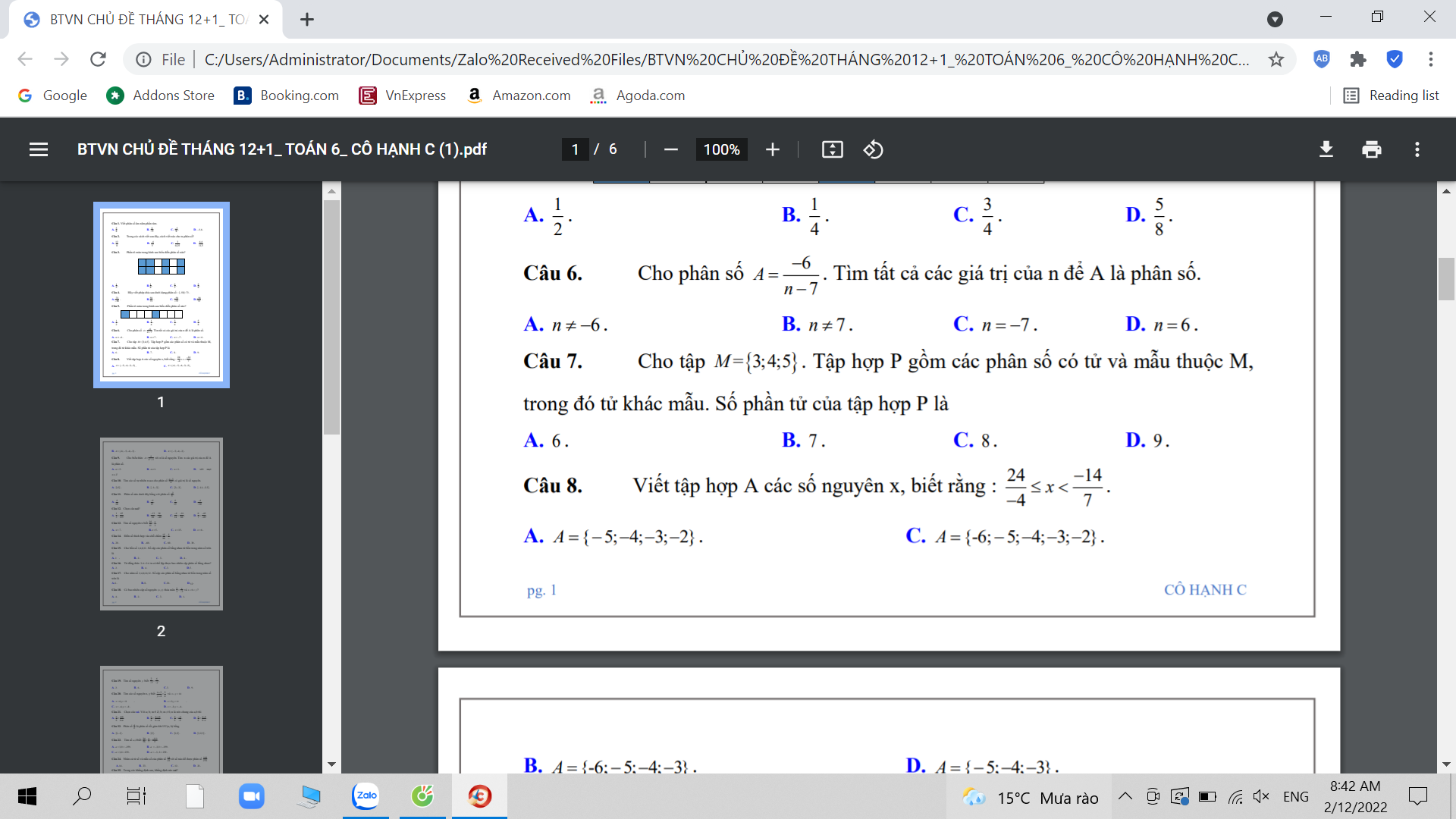 mọi người giúp em với ạ em đang cần gấp!!
mọi người giúp em với ạ em đang cần gấp!!









