Giúp em phần II ạ. Được bao nhiêu cx đc. Em xin cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,x+\dfrac{1}{2}=\dfrac{3}{4}\\ x=\dfrac{3}{4}-\dfrac{1}{2}\\ x=\dfrac{1}{2}\\ b,-\dfrac{2}{3}-x=1\\x=-\dfrac{2}{3}-1\\ x=-\dfrac{5}{3}\\ d,\dfrac{1}{4}+\dfrac{3}{4}:x=\dfrac{5}{2}\\ \dfrac{3}{4}:x=\dfrac{5}{2}-\dfrac{1}{4}\\ \dfrac{3}{4}:x=\dfrac{9}{4}\\ x=\dfrac{3}{4}:\dfrac{9}{4}\\ x=\dfrac{1}{3}\\ e,\left(x+\dfrac{1}{4}\right)\cdot\dfrac{3}{4}=-\dfrac{5}{8}\\ x+\dfrac{1}{4}=-\dfrac{5}{8}:\dfrac{3}{4}\\ x+\dfrac{1}{4}=\dfrac{5}{6}\\ x=\dfrac{5}{6}-\dfrac{1}{4}\\ x=\dfrac{7}{12}\)
\(g,\dfrac{x-3}{15}=\dfrac{-2}{5}\\ 5\left(x-3\right)=-30\\ x-3=-6\\ x=-6+3\\ x=-3\\ h,\dfrac{x}{-2}=\dfrac{-8}{x}\\ x^2=16\\ x=\pm\sqrt{16}\\ x=\pm4\\ k,\dfrac{x+2}{3}=\dfrac{x-4}{5}\\ 5\left(x+2\right)=3\left(x-4\right)\\ 5x+10=3x-12\\ 5x-3x=-12-10\\ 2x=-22\\ x=-11\)
\(m,\left(2x-1\right)^2=4\\ \Rightarrow\left[{}\begin{matrix}2x-1=2\\2x-1=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=3\\2x=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)

Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A

B
1 is writing
2 is losing
3 is having
4 is staying
5 amnot telling
6 is always using
7 are having
8 Are you playing
C
1 are top musicians studying => Do top musician study
2 don't touch => aren't touching
3 does
4 is Christine listening
5 am usually buying => usually buy
6 is starting => starts
7 Does your team win => is your team winning
8 are enjoying => enjoy

Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B

p: \(\dfrac{5}{1\cdot2}+\dfrac{5}{2\cdot3}+...+\dfrac{5}{50\cdot51}\)
\(=5\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{50\cdot51}\right)\)
\(=5\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{50}-\dfrac{1}{51}\right)\)
\(=5\cdot\left(1-\dfrac{1}{51}\right)=5\cdot\dfrac{50}{51}=\dfrac{250}{51}\)
q: \(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{1}{210}\)
\(=\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+...+\dfrac{2}{420}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{420}\right)\)
\(=2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{20\cdot21}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{20}-\dfrac{1}{21}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{21}\right)=2\cdot\dfrac{19}{42}=\dfrac{19}{21}\)

Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B



 giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ
giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ








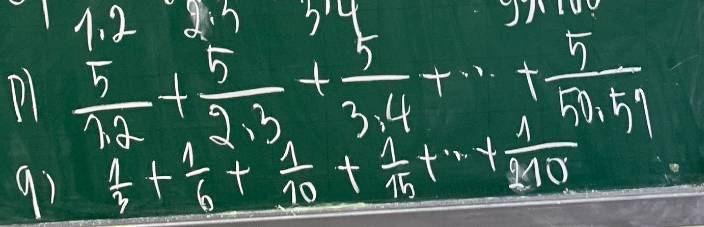




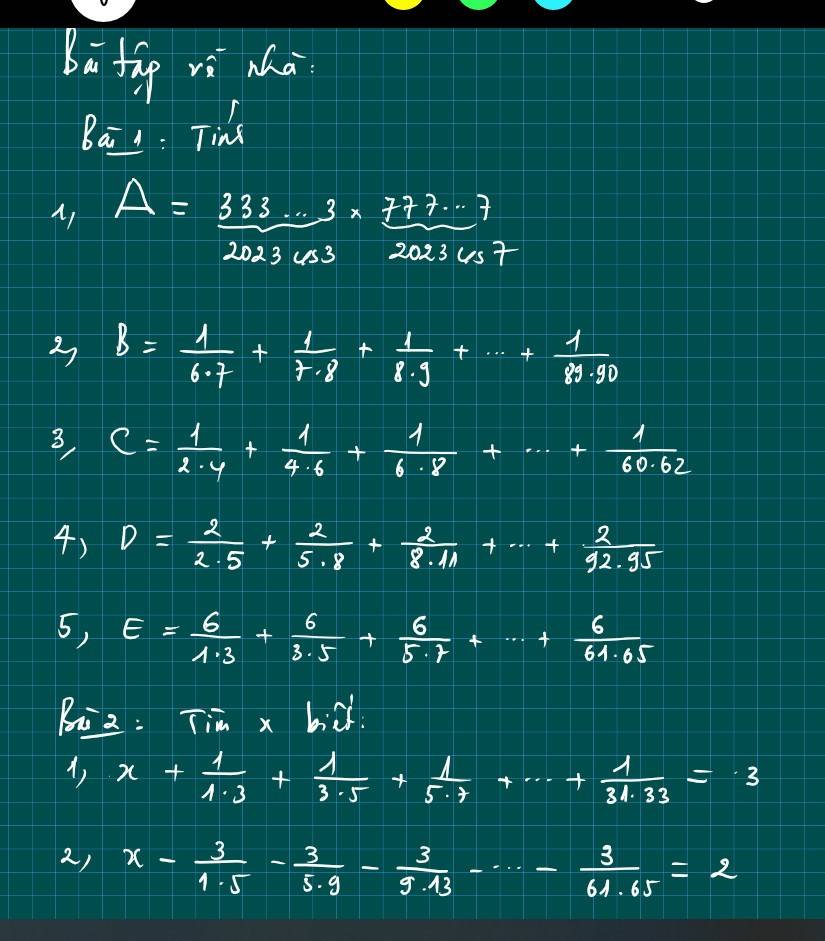
1) \(x^4-10x^2+1=0\)
\(\Leftrightarrow\left(x^2-5\right)^2=24\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-5=2\sqrt{6}\\x^2-5=-2\sqrt{6}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{5+2\sqrt{6}}\\x=\sqrt{5-2\sqrt{6}}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\\x=\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{3}+\sqrt{2}\\x=\sqrt{3}-\sqrt{2}\end{matrix}\right.\)
Vậy \(x=\sqrt{2}+\sqrt{3}\) là một nghiệm của pt
2) Ta có: \(a-b=\sqrt{3}+1,b-c=\sqrt{3}-1\)
\(\Rightarrow a-c=a-b+b-c=\sqrt{3}+1+\sqrt{3}-1=2\sqrt{3}\)
\(A=a^2+b^2+c^2-ab-bc-ac\)
\(\Rightarrow2A=2a^2+2b^2+2c^2-2ab-2ac-2bc\)
\(=\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(a^2-2ac+c^2\right)\)
\(=\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\)
\(\left(\sqrt{3}+1\right)^2+\left(\sqrt{3}-1\right)^2+\left(2\sqrt{3}\right)^2\)
\(=3+2\sqrt{3}+1+3-2\sqrt{3}+1+12=20\)
\(\Rightarrow A=10\in N\)