cho hình 3, biết Ax // Cy. chứng tỏ rằng góc A+C=ABC A B x C y Hình 3 ...
Đọc tiếp
cho hình 3, biết Ax // Cy. chứng tỏ rằng góc A+C=ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HL
1
25 tháng 9 2021
a) Ta có: \(\alpha+\widehat{ABm}=\alpha+180^0-\alpha=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Ax//Bm
b) Trên tia đối Bm kẻ Bn
=> Bn//Ax
\(\Rightarrow\alpha=\widehat{ABn}\)(so le trong)
\(\Rightarrow\widehat{CBn}=\widehat{ABC}-\widehat{ABn}=\alpha+\beta-\alpha=\beta\)
\(\Rightarrow\widehat{CBn}=\widehat{BCy}=\beta\)
Mà 2 góc này là 2 góc so le trong
=> Cy//Bm
PT
1
CM
14 tháng 5 2018
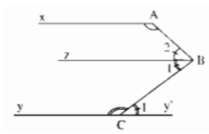
Kẻ Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ∠A +∠(B2 ) =180o
(2 góc trong cùng phía) (1)
Theo giả thiết ta có: ∠A +∠B + ∠C =360o (gt)
Hay ∠A +∠(B2 ) +∠(BCy) =360o (2)
Từ (1)và (2)suy ra :
∠(B1) + ∠BCy = 180o (3)
Lại có: ∠(C1 ) + ∠BCy =180o (hai góc kề bù) (4)
Từ (3) và (4) suy ra: ∠(B1 ) =∠(C1 )
Suy ra: Cy’ // Bz (vì có cặp góc so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra : Ax // Cy
NA
1
17 tháng 12 2023
Qua B kẻ tia Bz//Ax(Bz và Ax nằm khác phía so với đường thẳng AB)
Ta có: Bz//Ax
=>\(\widehat{zBA}=\widehat{xAB}\)
Ta có: \(\widehat{zBA}+\widehat{zBC}=\widehat{ABC}\)
\(\widehat{xAB}+\widehat{yCB}=\widehat{ABC}\)
mà \(\widehat{zBA}=\widehat{xAB}\)
nên \(\widehat{zBC}=\widehat{yCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Bz//Cy
mà Ax//Bz
nên Ax//Cy
PT
1
CM
20 tháng 2 2018
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy.
Ta có: ∠(B2 ) +∠(xAB) =180o
(hai góc trong cùng phía)
Mà ∠(xAB) =140o(gt)
Suy ra: ∠(B2 ) =180-∠(xAB) =180o-140o=40o
Mà: ∠(B1 ) +∠(B2 ) =∠(ABC)
Suy ra ∠(B1 ) =∠(ABC) -(B2 ) =70o-40o=30o (1)
∠(yCB) +∠(BCy') =180o(2 góc kề bù)
∠BCy'=180o-∠(yCB) =180o-150o=30o (2)
Từ (1) và (2) ta có: ∠(B1 ) =∠(BCy')
Suy ra: Cy’ // Bz ( vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra Ax // Cy