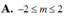Tìm x,y\(\in\)N để 2x2-3x+4 =y2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Sửa đề:
\(3x^2-\sqrt3 x+\dfrac14(dkxd:x\geq0)\\=(x\sqrt3)^2-2\cdot x\sqrt3\cdot\dfrac12+\Bigg(\dfrac12\Bigg)^2\\=\Bigg(x\sqrt3-\dfrac12\Bigg)^2\)
b,
\(x^2-x-y^2+y\\=(x^2-y^2)-(x-y)\\=(x-y)(x+y)-(x-y)\\=(x-y)(x+y-1)\)
c,
\(x^4+x^3+2x^2+x+1\\=(x^4+x^3+x^2)+(x^2+x+1)\\=x^2(x^2+x+1)+(x^2+x+1)\\=(x^2+x+1)(x^2+1)\)
d,
\(x^3+2x^2+x-16xy^2\\=x(x^2+2x+1-16y^2)\\=x[(x+1)^2-(4y)^2]\\=x(x+1-4y)(x+1+4y)\\Toru\)

\(a.\left(x^2+4x+4\right)+\left(x^2-6x+9\right)=2x^2+14x\)
\(x^2+4x+4+x^2-6x+9-2x^2-14x=0\)
\(-18x+13=0\)
\(x=\dfrac{13}{18}\)
Vậy \(S=\left\{\dfrac{13}{18}\right\}\)
\(b.\left(x-1\right)^3-125=0\)
\(\left(x-1\right)^3=125\)
\(x-1=5\)
\(x=6\)
Vậy \(S=\left\{6\right\}\)
\(c.\left(x-1\right)^2+\left(y +2\right)^2=0\)
\(Do\left(x-1\right)^2\ge0\forall x;\left(y+2\right)^2\ge0\forall y\)
\(\Rightarrow\left(x-1\right)^2+\left(y+2\right)^2\ge0\forall x,y\)
Mà \(\left(x-1\right)^2+\left(y+2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Vậy \(S=\left\{1;-2\right\}\)
\(d.x^2-4x+4+x^2-2xy+y^2=0\)
\(\left(x-2\right)^2+\left(x-y\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-2\right)^2=0\\\left(x-y\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Vậy \(S=\left\{2;2\right\}\)

\(a,\left(x^3+5x^2-2x+1\right)\left(x-7\right)\\ =x^4-7x^3+5x^3-35x^2-2x^2+14x+x-7\\ =x^4-2x^3-37x^2+15x-7\\ b,\left(2x^2-3xy+y^2\right)\left(x+y\right)\\ =2x^3+2x^2y-3x^2y-3xy^2+xy^2+y^3\\ =2x^3-x^2y-2xy^2+y^3\\ c,\left(x-2\right)\left(x^2-5x+1\right)-x\left(x^2+11\right)\\ =x^3-5x^2+x-2x^2+10x--x^3-11x\\ =x^3-7x^2\\ d,x\left(1-3x\right)\left(4-3x\right)-\left(x-4\right)\left(3x+5\right)\\ =x\left(4-15x+9x^2\right)-\left(3x^2-7x-20\right)\\ =4x-15x^2+9x^3-3x^2+7x+20\\ =9x^3-18x^2+11x+20\)

\(\Leftrightarrow\left(x^2+2xy+y^2\right)+4\left(x+y\right)+4+\left(x^2-12x+36\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2+4\left(x+y\right)+4+\left(x-6\right)^2=0\)
\(\Leftrightarrow\left(x+y+2\right)^2+\left(x-6\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\x+y+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=-8\end{matrix}\right.\)
\(y^2+2xy-12x+4\left(x+y\right)+2x^2+40=0\\ \Leftrightarrow\left[\left(x^2+2xy+y^2\right)+4\left(x+y\right)+4\right]+\left(x^2-12x+36\right)=0\\ \Leftrightarrow\left(x+y+2\right)^2+\left(x-6\right)^2=0\)
Vì \(\left\{{}\begin{matrix}\left(x+y+2\right)^2\ge0\forall x,y\\\left(x-6\right)^2\ge0\forall x\end{matrix}\right.\)
Nên \(\left(x+y+2\right)^2+\left(x-6\right)^2\ge0\forall x,y\)
Dấu"=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}x+y+2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-8\\x=6\end{matrix}\right.\)
Vậy x = 6 và y = -8

a) 2x. (x2 – 7x -3)
= 2x3- 14x2- 6x
b) ( -2x3 + y2 -7xy). 4xy2
= -8x4y2+ 4xy4- 28x2y3
c)(-5x3).(2x2+3x-5)
= -10x5-15x4+25x3
d) (2x2 - xy+ y2).(-3x3)
=-6x5+ 3x4y -3x3y2
e)(x2 -2x+3). (x-4)
=x3-2x2+3x -4x2+8x-12
=x3-6x2+11x-12
f) ( 2x3 -3x -1). (5x+2)
=10x4-15x2-5x +4x3-6x-2
=10x4+4x3-15x2-11x-2

Xét biểu thức \(A=x\left(x-3\right)\left(x-4\right)\left(x-7\right)=\left(x^2-7x\right)\left(x^2-7x+12\right)\)
Đặt \(x^2-7x+6\rightarrow t\)Khi đó \(A=\left(t-6\right)\left(t+6\right)=t^2-36\ge-36\)
Dấu "=" xảy ra khi và chỉ khi \(t=0\)hay \(x^2-7x+6=0=>\left(x-6\right)\left(x-1\right)=0=>\orbr{\begin{cases}x=6\\x=1\end{cases}}\)
Vậy GTNN của biểu thức \(A=-36\)đạt được khi \(x=6orx=1\)
Xét biểu thức \(B=2x^2+y^2-2xy-2x+3=\left(x^2-2xy+y^2\right)+x^2-2x+1+2\)
\(=\left(x-y\right)^2+\left(x-1\right)^2+2\ge2\)
Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-y=0\\x-1=0\end{cases}< =>\hept{\begin{cases}1-y=0\\x=1\end{cases}}< =>\hept{\begin{cases}x=1\\y=1\end{cases}< =>x=y=1}}\)
Vậy GTNN của biểu thức \(B=2\)đạt được khi \(x=y=1\)

Phương trình 1 ⇔ x + y 2 x - y = 0 ⇔ x = − y 2 x = y
Trường hợp 1: x = - y thay vào (2) ta được x 2 - 4 x + 3 = 0 ⇔ x = 1 x = 3
Suy ra hệ phương trình có hai nghiệm là (1; −1), (3; −3).
Trường hợp 2: 2 x = y thay vào (2) ta được - 5 x 2 + 17 x + 3 = 0 phương trình này không có nghiệm nguyên.
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; −1) và (3; −3).
Đáp án cần chọn là: C