cho tam giác ABC, các trung tuyến BD và CE. Gọi i,k là giao điểm của mn với BD,EC
a. CMR: MI=KN
b. CMR: MI=ik=kn
cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
20 tháng 9 2020
1)\(\Delta\)ABC có E là trung điểm của AB, D là trung điểm của AC nên ED là đường trung bình của tam giác => ED//BC
Tứ giác EDCB có ED//BC nên là hình thang (đpcm)
2) Hình thang EDCB có M, N lần lượt là trung điểm của BE và CD nên MN là đường trung bình của hình thang => MN // ED hay \(\hept{\begin{cases}NK//ED\\MI//ED\end{cases}}\)
\(\Delta\)BED có M là trung điểm của BE và MI//ED nên I là trung điểm của BD
Tương tự ta suy ra được K là trung điểm của CE
c) Ta có: IK = IN - KN = 1/2BC - 1/2ED = \(\frac{BC-ED}{2}=\frac{BC-\frac{BC}{2}}{2}=\frac{\frac{BC}{2}}{2}=\frac{BC}{4}\)
\(KN=MI=\frac{ED}{2}=\frac{\frac{BC}{2}}{2}=\frac{BC}{4}\)
Từ đó suy ra MI = IK = KN (đpcm)
CM
13 tháng 1 2017
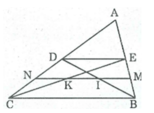
Trong ∆ ABC ta có: E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ ED // BC và ED = 1/2 BC
(tính chất đường trung bình của tam giác)
+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE
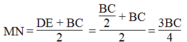
(tính chất đường trung bình hình thang)
Trong ∆ BED, ta có: M là trung điểm BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
Trong ∆ CED ta có: N là trung điểm CD
NK // DE
Suy ra: NK là đường trung bình của ∆ CED
⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC
⇒ MI = IK = KN = 1/4 BC
13 tháng 7 2018
a) Xét \(\Delta ABC\)có \(AE=EB\)
\(AD=DC\)
\(\Rightarrow\)ED là đường trung bình \(\Delta ABC\)
\(\Rightarrow\hept{\begin{cases}ED=\frac{1}{2}BC\Leftrightarrow ED=\frac{1}{2}\times8=4\left(cm\right)\\ED//BC\end{cases}}\)
\(\Rightarrow\)EDCB là hình thang
Lại có : \(EM=MB\)
\(DN=NC\)
\(\Rightarrow\)MN là đường trung bình của hình thang EDCB
\(\Rightarrow MN=\frac{ED+BC}{2}=\frac{4+8}{2}=\frac{12}{2}=6\left(cm\right)\)
Vậy \(MN=6cm\)
b) Xét \(\Delta BED\)có M là trung điểm BE ; MI // ED
\(\Rightarrow\)MI là dường trung bình \(\Delta BED\)
\(\Rightarrow MI=\frac{1}{2}ED=\frac{1}{2}\times4=2\left(cm\right)\)
Xét \(\Delta CED\)có N là trung điểm CD ; NK // ED
\(\Rightarrow\)NK là đường trung bình \(\Delta CED\)
\(\Rightarrow NK=\frac{1}{2}ED=\frac{1}{2}\times4=2\left(cm\right)\)
Lại có : \(MI+IK+KN=MN\)
\(\Leftrightarrow2+IK+2=6\)
\(\Leftrightarrow IK=2\left(cm\right)\)
Vậy \(MI=IK=KN\left(=2cm\right)\)
30 tháng 6 2017
1) Bài 38 Sách bài tập - trang 84 - Toán lớp 8 | Học trực tuyến
2) Bài 40 Sách bài tập - trang 84 - Toán lớp 8 | Học trực tuyến.
DN
30 tháng 8 2018
1,Trong tam giác ABC ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của tam giác ABC
⇒ED // BC và \(ED=\dfrac{BC}{2}\) (tính chất đường trung bình của tam giác) \(^{\left(1\right)}\)
Trong tam giác GBC ta có:
I là trung điểm của BG (gt)
K là trung điểm của CG (gt)
Nên IK là đường trung bình của ∆ GBC
⇒ IK // BC và \(IK=\dfrac{BC}{2}\) (tính chất đường trung bình của tam giác) \(^{\left(2\right)}\)
Từ (1) và (2) suy ra: IK // DE và IK = DE.
2,Trong tam giác ABC ta có:
-E là trung điểm của cạnh AB
-D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
\(\Rightarrow ED//BC\) và \(ED=\dfrac{1}{2}BC\) (tính chất đường trung bình của tam giác)
Trong hình thang BCDE, ta có: BC // DE
-M là trung điểm cạnh bên BE
-N là trung điểm cạnh bên CD
Nên MN là đường trung bình hình thang BCDE ⇒ MN // DE
\(MN=\dfrac{DE+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3BC}{4}\) (tính chất đường trung bình hình thang)
Trong tam giác BED ta có:
M là trung điểm của BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
\(\Rightarrow MI=\dfrac{1}{2}DE=\dfrac{1}{4}BC\) (tính chất đường trung bình tam giác)
Trong tam giác CED ta có:
N là trung điểm của CD
NK // DE
Suy ra: NK là đường trung bình của ∆ BED
\(\Rightarrow NK=\dfrac{1}{2}DE=\dfrac{1}{4}BC\) (tính chất đường trung bình tam giác)
\(IK=MN-\left(MI+NK\right)\)
\(=\dfrac{3}{4}BC-\left(\dfrac{1}{4}BC+\dfrac{1}{4}BC\right)=\dfrac{1}{4}BC\)
\(\Rightarrow MI=IK=KN=\dfrac{1}{4}BC\)
28 tháng 7 2018
Bài 40 Sách bài tập - trang 84 - Toán lớp 8 | Học trực tuyến bạn tham khảo thêm ở link này nhé hoặc là bạn có thể vào mục tìm các câu hỏi tương tự! Nhiều bạn giải rồi nên mình sẽ không làm nữa. Chúc bạn học tốt :))
28 tháng 7 2018
Đặt BC=a
Vì △ABC có AE=BE, AD=DC nên ED là đường trung bình , do đó ED// BC, ED=\(\dfrac{BC}{2}=\dfrac{a}{2}\)
Do MN là đường trung bình của tứ giác EDCB, nên MN//ED//BC.
- △BED có M là trung điểm của BE, MI//ED nên MI là đường trung bình của tam giác BED, do đó MI=\(\dfrac{ED}{2}=\dfrac{a}{4}\)(1)
-△CED có N là trung điểm của CD, NK//ED nên NK là đường trung bình cuả tam giác CED, đ=do đó NK=\(\dfrac{ED}{2}=\dfrac{a}{4}\)(2)
- △BEC có M là trung điểm của BE, MK//BC nên MK là đường trung bình của tam giác BEC, do đó MK=\(\dfrac{BC}{2}=\dfrac{a}{2}\)
Ta có IK=MK-MI=\(\dfrac{a}{2}-\dfrac{a}{4}=\dfrac{a}{4}\)(3)
Từ (1),(2) và (3) ta có MI=NK=IK ( đpcm )
4 tháng 9 2017
Bạn ơi hình như đề sai chứ mk làm 1 bài là IK bằng ED cơ, mà có định lý này nè: Đường trung bình đi qua trung điểm 2 đường chéo của hình thanh thì đoạn nối 2 trung điểm đó bằng đáy nhỏ của hình thang mà. Nếu có sách học tốt toán lớp 8 thì bạn xem bài 60 trang 122 nhé!