Cho hai tập hợp
U = [ x2 - 2x; 2x2 - 4x + 5] (x∈R)
V = {y ∈ R/ |y2 - 4y - 5|≥3}
Tìm x để:
a) U có độ dài nhỏ nhất.
b) U và { |t - 1|>2} rời nhau
C) U giao CRV ≠ ∅
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{2x}{x^2+1}\ge1\Leftrightarrow2x\ge x^2+1\Leftrightarrow x^2-2x+1\le0\\ \Leftrightarrow\left(x-1\right)^2\le0\)
Mà \(\left(x-1\right)^2\ge0\Leftrightarrow x-1=0\Leftrightarrow x=1\)
\(A=\left\{1\right\}\)
Để \(x^2-2bx+4=0\Leftrightarrow\Delta=4b^2-4\cdot4< 0\)
\(\Leftrightarrow b^2-4< 0\Leftrightarrow\left(b-2\right)\left(b+2\right)< 0\\ \Leftrightarrow x\le-2;x\ge2\)
\(\Leftrightarrow B=\left\{x\in R|x\le-2;x\ge2\right\}\)
Vậy \(A\cap B=\varnothing\)

Câu 2:
\(\left(A\cup B\right)\cap C=A\cap C=[1;+\infty)\cap\left(0;4\right)=[1;4)\)
Tập này có 3 phần tử nguyên

Đáp án: C
A = {0;-1;1}; B = {0;-1;3}
A ∪ B = {0;-1;1;3}; A ∩ B = {0;-1}
(A ∪ B) \ (A ∩ B) = {1;3} => có 2 phần tử.

Gọi x 1 , x 2 là nghiệm của phương trình x 2 - 2 m x + 1 = 0 . Khi đó x 1 + x 2 = 2 m x 1 . x 2 = 1
Gọi
x
3
,
x
4
là nghiệm của phương trình
x
2
-
2
m
x
+
1
=
0
. Khi đó
x
3
+
x
4
=
2
x
3
.
x
4
=
m
Ta có: x 1 = 1 x 3 x 2 = 1 x 4 ⇒ x 1 + x 2 = 1 x 3 + 1 x 4 x 1 . x 2 = 1 x 3 . x 4
⇒ x 1 + x 2 = x 3 + x 4 x 3 . x 4 x 1 . x 2 = 1 x 3 . x 4 ⇔ 2 m = 2 m 1 = 1 m ⇔ m = 1
Đáp án cần chọn là: C

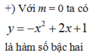
Hàm số y = - x 2 + 2 x + không nghịch biến trên ℝ ⇒ m = 0 không thỏa mãn
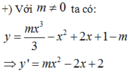
Để hàm số nghịch biến trên ℝ thì
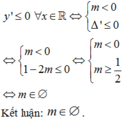
Chọn: D

a. M={26; 28; 30;...; 140; 142}
Số phần tử của M là:
( 142 - 26 ) : 2 + 1 = 59 (phần tử)
b. Tập hợp con của H:
\(\phi\); {a}; {5}; {x}; {a;5}; {a;x}; {5;x}; {a;5;x}.
Tập hợp con của K :
\(\phi\); {c}; {y}; {8}; {x}; {c;y} ;{c;8} ; {c;x}; {y;8} ; {y;x} ; {8;x}; {c;y;8} ; {c;y;x}; {c;8;x}; {y;8;x}; {c;y;8;x}.