hình thang có nhiều nhất hai góc tù , thì có nhiều nhất bao nhiêu góc nhọn bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có nhiều nhất 2 góc tù và 2 góc nhọn
Xét hình thang ABCD co AB//CD
Nhu vay: goc A + goc D =180 do va goc B +goc C =180 do
- Neu goc A tu (> 90do) => goc D nhon
- Neu goc B tu => goc C nhon
Nen trong 1 hinh thang chi co toi da 2 goc tu

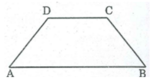
Xét hình thang ABCD có AB //CD.
Ta có:
* ∠ A và ∠ D là hai góc kề với cạnh bên
⇒ ∠ A + ∠ D = 180 0 (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.
* ∠ B và ∠ C là hai góc kề với cạnh bên
⇒ ∠ B + ∠ C = 180 0 (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.
Vậy trong bốn góc là A, B, C, D có nhiều nhất là hai góc tù và có nhiều nhất là hai góc nhọn.

1 )
Xét hình thang ABCD (AB//CD)
góc A + góc D =180 độ (2 góc trong cùng phía )
góc B +góc C =180 độ
- Nếu góc A tù (> 90độ) => góc D nhọn
- Nếu góc B tú => góc C nhọn
=> hình thang có nhiều nhất 2 góc tù, có nhiều nhất 2 góc nhọn
2 ) Giả sử ABCD là hình thang có đáy AB//CD
Khi đó ta có góc A + góc D bằng 180 độ (2 góc kề 1 cạnh bên hình thang bù nhau) (Hoặc bạn hiểu là 2 góc trong cùng phía bù nhau đó)
Vậy tia phân giác góc A nên bằng nửa góc A
TIa phân giác góc D bằng nửa góc D
Vậy Cộng 2 góc tia phân giác đó bằng 180độ chia 2 bằng 90 độ
2,
Giả sử ABCD là hình thang có đáy AB//CD
Khi đó ta có góc A + góc D bằng 180 độ (2 góc kề 1 cạnh bên hình thang bù nhau) (Hoặc bạn hiểu là 2 góc trong cùng phía bù nhau đó)
Vậy tia phân giác góc A nên bằng nửa góc A
TIa phân giác góc D bằng nửa góc D
Vậy Cộng 2 góc tia phân giác đó bằng 180 độ chia 2 bằng 90 độ

A B C D
Xét hình thang ABCD có AB// CD
\(\widehat{A},\widehat{D}\) là hai góc kề với cạnh bên.
\(\Rightarrow\widehat{A}+\widehat{D}=180^o\) (do 2 góc trong cùng phía )
Nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.
\(\widehat{B},\widehat{C}\) là hai góc kề với cạnh bên.
\(\Rightarrow\widehat{B}+\widehat{C}=180^o\) (do 2 góc trong cùng phía )
Nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất 1 góc tù.
Vậy bốn góc là : \(\widehat{A},\widehat{B},\widehat{C},\widehat{D}\) có nhiều nhất là hai góc nhọn và nhiều nhất là hai góc tù.

xét hình thang ABCD(AB//CD)
góc A + gốc D =180 độ(2 góc trong cùng phía)
góc B +góc C = 180 độ
- nếu góc A tù(>90 độ) =>góc D nhọn
- nếu góc B tù(>90 độ)=> góc C
=> hình thang có nhiều nhất 2 góc tù và 2 góc nhọn
