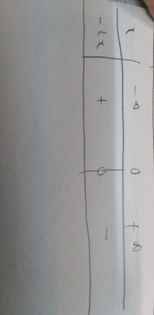
Lập bảng xét dấu nhị thức bậc nhất của:
a) f(x) = 3x-5
b) f(x) = 2x+4
c) f(x) = -x+1
d) f(x) = -2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Ta có \(a = 3 > 0,b = - 4,c = 1\)
\(\Delta ' = {\left( { - 2} \right)^2} - 3.1 = 1 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\). Khi đó:
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( { - \infty ;\frac{1}{3}} \right)\) và \(\left( {1; + \infty } \right)\);
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( {\frac{1}{3};1} \right)\)
b) Ta có \(a = 9 > 0,b = 6,c = 1\)
\(\Delta ' = 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 1 nghiệm \(x = - \frac{1}{3}\). Khi đó:
\(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\backslash \left\{ { - \frac{1}{3}} \right\}\)
c) Ta có \(a = 2 > 0,b = - 3,c = 10\)
\(\Delta = {\left( { - 3} \right)^2} - 4.2.10 = - 71 < 0\)
\( \Rightarrow \)\(f\left( x \right) > 0\forall x \in \mathbb{R}\)
d) Ta có \(a = - 5 < 0,b = 2,c = 3\)
\(\Delta ' = {1^2} - \left( { - 5} \right).3 = 16 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = \frac{{ - 3}}{5},x = 1\). Khi đó:
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( { - \infty ; - \frac{3}{5}} \right)\) và \(\left( {1; + \infty } \right)\);
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( { - \frac{3}{5};1} \right)\)
e) Ta có \(a = - 4 < 0,b = 8c = - 4\)
\(\Delta ' = 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 1 nghiệm \(x = 1\). Khi đó:
\(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\backslash \left\{ 1 \right\}\)
g) Ta có \(a = - 3 < 0,b = 3,c = - 1\)
\(\Delta = {3^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = - 3 < 0\)
\( \Rightarrow \)\(f\left( x \right) < 0\forall x \in \mathbb{R}\)
QT
1
23 tháng 9 2023
Tham khảo:
Tam thức bậc hai \(f\left( x \right) = - {x^2} - 2x + 8\) có hai nghiệm phân biệt \({x_1} = - 4,{x_2} = 2\) và hệ số \(a = - 1 < 0\).
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
PT
1
CM
18 tháng 6 2017
Nhị thức 3x + 2 có nghiệm là: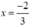 
. Bảng xét dấu của f(x)= 3x + 2:
Nhị thức – 2x + 5 có nghiệm là: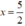 
. Bảng xét dấu của g(x) = -2x + 5
17 tháng 2 2022
b: \(\Delta=2^2-4\cdot1\cdot1=0\)
Do đó: Tam thức này dương khi x khác -1; bằng 0 khi x=-1
a: \(\Delta=3^2-4\cdot\left(-5\right)\cdot\left(-1\right)=9-20=-11< 0\)
Do đó: Tam thức này luôn âm với mọi x
c: \(\Delta=1^2-4\cdot1\cdot\left(-2\right)=9\)
Do đó: Tam thức này âm khi -2<x<1
Bằng 0 khi x=-2 hoặc x=1
Dương khi x<-2 hoặc x>1
23 tháng 9 2023
Tham khảo:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:
b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:
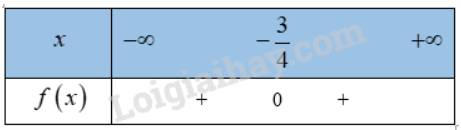
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:
9 tháng 9 2021
\(a,f\left(1\right)=3\cdot1^2+1+1=5\\ f\left(-\dfrac{1}{3}\right)=3\cdot\left(-\dfrac{1}{3}\right)^2-\dfrac{1}{3}+1=\dfrac{1}{3}-\dfrac{1}{3}+1=1\\ f\left(\dfrac{2}{3}\right)=3\cdot\left(\dfrac{2}{3}\right)^2-\dfrac{2}{3}+1=\dfrac{4}{3}-\dfrac{2}{3}+1=\dfrac{5}{3}\\ f\left(-2\right)=3\cdot\left(-2\right)^2-2+1=11\\ f\left(-\dfrac{4}{3}\right)=3\cdot\left(-\dfrac{4}{3}\right)^2-\dfrac{4}{3}+1=\dfrac{16}{3}-\dfrac{4}{3}+1=5\)
\(b,f\left(\dfrac{2}{3}\right)=\left|2\cdot\dfrac{2}{3}-9\right|-3=\dfrac{23}{3}-3=\dfrac{14}{3}\\ f\left(-\dfrac{5}{4}\right)=\left|2\cdot\left(-\dfrac{5}{4}\right)-9\right|-3=\dfrac{23}{2}-3=\dfrac{17}{2}\\ f\left(-5\right)=\left|2\left(-5\right)-9\right|-3=19-3=16\\ f\left(4\right)=\left|2\cdot4-9\right|-3=1-3=-2\\ f\left(-\dfrac{3}{8}\right)=\left|2\cdot\left(-\dfrac{3}{8}\right)-9\right|-3=\dfrac{39}{4}-3=\dfrac{27}{4}\)
9 tháng 9 2021
\(c,x=0\Rightarrow y=2\cdot0^2-7=-7\\ x=-3\Rightarrow y=2\cdot\left(-3\right)^2-7=11\\ x=-\dfrac{1}{2}\Rightarrow y=2\cdot\left(-\dfrac{1}{2}\right)^2-7=\dfrac{-13}{2}\\ x=\dfrac{2}{3}\Rightarrow y=2\cdot\left(\dfrac{2}{3}\right)^2-7=-\dfrac{55}{9}\)
20 tháng 3 2023
a) Ta có:
\(f\left(x\right)=2x^3-x^5+3x^4+x^2-\dfrac{1}{2}x^3+3x^5-2x^2-x^4+1\)
\(f\left(x\right)=\left(-x^5+3x^5\right)+\left(3x^4-x^4\right)+\left(2x^3-\dfrac{1}{2}x^3\right)+\left(x^2-2x^2\right)+1\)
\(f\left(x\right)=2x^5+2x^4+\dfrac{3}{2}x^3-x^2+1\)
Sắp xếp đa thức f(x) the lũy thừa giảm dần của biến, ta được:
\(f\left(x\right)=2x^5+2x^4+\dfrac{3}{2}x^3-x^2+1\)
b) Bậc của đa thức f(x) là 5
c) Ta có:
\(f\left(1\right)=2\cdot1^5+2\cdot1^4+\dfrac{3}{2}\cdot1^3-1^2+1=5,5\) . Vậy f(1) = 5,5.
\(f\left(-1\right)=2\cdot\left(-1\right)^5+2\cdot\left(-1\right)^4+\dfrac{3}{2}\cdot\left(-1\right)^3-\left(-1\right)^2+1=-1,5\). Vậy f(-1) = -1,5.
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) \(f\left( x \right) = 2{x^2} + 4x + 2\) có \(\Delta = 0\), có nghiệm kép là \({x_1} = {x_2} = - 1\)
và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
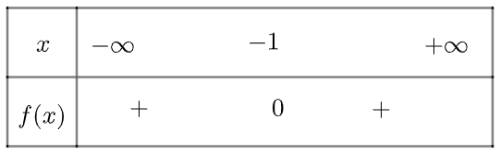
Vậy \(f\left( x \right)\) dương với mọi \(x \ne - 1\)
b) \(f\left( x \right) = - 3{x^2} + 2x + 21\) có \(\Delta = 256 > 0\), hai nghiệm phân biệt là \({x_1} = - \frac{7}{3};{x_2} = 3\)
và \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
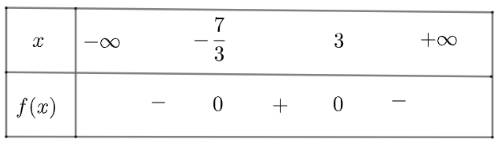
Vậy \(f\left( x \right)\) dương với \(x \in \left( { - \frac{7}{3};3} \right)\) và âm khi \(x \in \left( { - \infty ; - \frac{7}{3}} \right) \cup \left( {3; + \infty } \right)\)
c) \(f\left( x \right) = - 2{x^2} + x - 2\) có \(\Delta = - 15 < 0\), tam thức vô nghiệm
và \(a = - 2 < 0\)
Ta có bảng xét dấu như sau:
Vậy \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
d) \(f\left( x \right) = - 4x\left( {x + 3} \right) - 9 = - 4{x^2} - 12x - 9\) có \(\Delta = 0\), tam thức có nghiệm kép \({x_1} = {x_2} = - \frac{3}{2}\) và \(a = - 4 < 0\)
Ta có bảng xét dấu như sau
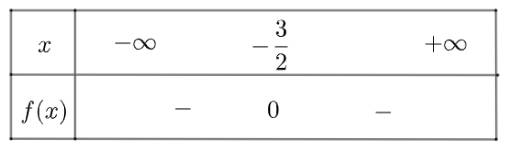
Vậy \(f\left( x \right)\) âm với mọi \(x \ne - \frac{3}{2}\)
e) \(f\left( x \right) = \left( {2x + 5} \right)\left( {x - 3} \right) = 2{x^2} - x - 15\) có \(\Delta = 121 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{5}{2};{x_2} = 3\) và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
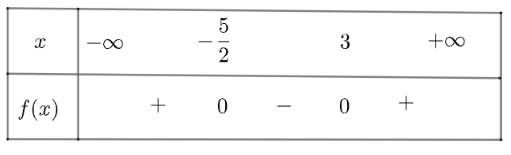
Vậy \(f\left( x \right)\) âm với \(x \in \left( { - \frac{5}{2};3} \right)\) và dương khi \(x \in \left( { - \infty ; - \frac{5}{2}} \right) \cup \left( {3; + \infty } \right)\)
a
b:
c:
d: