6.Tổng 2 lập phương
?1:tính (a + b) (a2- ab + b2)
?2: phát biểu hằng đẳng thức số 6 bằng lời
7.Hiệu 2 lập phương
?3: tính ( a- b )(a2 + ab +b2 )
?4:phát biể hằng đẳng thwasc số 7 bằng lời
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
0
VS
6 tháng 4 2017
bai 1
=ax5-x5-9xy-4xy-7x
=ax5-(5x+7x)-(9xy+4xy)
=5ax-12x-13xy
2
M=4a+ab-2b+2a-2b+ab
=6a+2ab-4b
n=6a+2b-ab+2a
=8a+2b-ab
m-n=6a+2ab-4b-8a-2b+ab
=3ab-2a-6b
13 tháng 6 2023
2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
23 tháng 10 2016
bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....
CM
20 tháng 8 2019
Ta có:
f(x) = x4 – x2 + 6x – 9 = x4 – (x2 – 6x +9) = – (x-3)2
= (x2 –x + 3).(x2 + x - 3)
+ Tam thức x2 – x + 3 có Δ = -11 < 0, a = 1 > 0 nên x2 – x + 3 > 0 với ∀ x ∈ R.
+ Tam thức x2 + x – 3 có hai nghiệm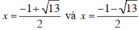 
Ta có bảng xét dấu sau:
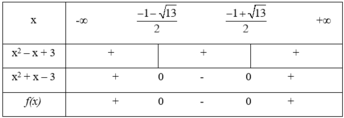
Kết luận:
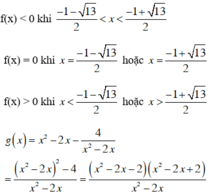
Tam thức x2 - 2x + 2 có Δ = -4 < 0, hệ số a = 1 > 0 nên x2 - 2x + 2 > 0 với ∀ x ∈ R
Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3.
Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2
Ta có bảng xét dấu :
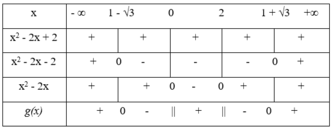
Kết luận : g(x) < 0 khi x ∈ (1 - √3; 0) ∪ (2; 1 + √3)
g(x) = 0 khi x = 1- √3 hoặc x = 1 + √3
g(x) > 0 khi x ∈ (-∞; 1 - √3) ∪ (0; 2) ∪ (1 + √3; +∞)
g(x) không xác định khi x = 0 và x = 2.
Mấy cái này ở trong sách có hết mà bạn :>
6.
?1
(a + b) (a2 - ab + b2)
= a3 - a2b + ab2 + a2b - ab2 +b3
= a3 - b3
?2 HĐT số 6: Lập phương của 1 tổng
Lập phương của 1 tổng bằng lập phương số thứ nhất cộng 3 lần tích bình phương số thứ nhất với số thứ hai cộng 3 lần tích số thứ nhất với bình phương số thứ hai cộng lập phương số thứ ba.
7.
?3
(a - b)(a2 + ab +b2)
= a3 + a2b + ab2 - a2b - ab2 - b3
= a3 - b3
?4 HĐT số 7: Lập phương của 1 hiệu:
Lập phương của 1 hiệu bằng lập phương số thứ nhất trừ 3 lần tích bình phương số thứ nhất với số thứ hai cộng 3 lần tích số thứ nhất với bình phương số thứ hai trừ lập phương số thứ ba.
_Moonlight_