Hãy nêu cách chứng minh hệ thức Vi-ét ?
HELP ME PLEZ !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
I
3
Những câu hỏi liên quan
HQ
2
27 tháng 9 2023
+ Delta là một chữ cái trong bảng chữ Hy Lạp, được kí hiệu là Δ (đối với chữ hoa) và δ (đối với chữ thường).
+ Trong toán học, đặc biệt là Toán 9, ký hiệu Δ chỉ một biệt thức trong phương trình bậc hai mà dựa vào từng giá trị của delta ta có thể kết luận được số nghiệm của phương trình bậc hai.
+ Ngoài ra delta còn dùng để kí hiệu cho đường thẳng mà các bạn sẽ được học ở các lớp cao hơn.
H
5 tháng 5 2022
Tham khảo
Qua tác phẩm Sống chết mặc bay thì dường như Phạm Duy Tốn đã khác họa thành công và rõ nét nhất thái độ vô trách nhiệm, bàn quan của tên quan phụ mẫu, xây dựng chân thật nhất một tên quan"lòng lang dạ sói". Hãy thử tưởng tượng mà xem, khi những con dân của mình đang "chân lấm tay bùn, trăm lo nghìn sợ, đem thân yếu hèn mà đối với sức mưa to nước lớn, để bảo thủ lấy tính mạng gia tài" thì quan phụ mẫu - người phải chăm lo việc này lại đang say sưa trong ván bài. Với hắn, có lẽ những ván bài đỏ đen còn quan trọng gấp vạn lần tính mạng của con dân. Ôi thôi, liệu cái ván bài đó có đáng để hi sinh hơn mấy trăm mạng ngươi chứ! Thật đúng là một tên vô lại! Mà ấy còn chưa hết, thậm chí khi "đứa con" của ngài chạy vào nói: "Bẩm...quan lớn...đê vỡ mất rồi!", hắn còn quát vào mặt, đe doạ: "....Đê vỡ rồi, thời ông cách cổ chúng, thời ông bỏ tù …..! Có biết không?..." rồi đuổi ra. Thật đúng là một kẻ vô lương tâm, độc ác! Phải nói rằng, tác phẩm Sống chết mặc bay chính là một tác phẩm lên án cái xã hội phong kiến thối nát một cách triệt để nhất.
CM
19 tháng 5 2018
2 x 2 + 9x + 7 = 0
∆ = 9 2 - 4.2.7 = 81 - 56 = 25 > 0
Do đó, phương trình có hai nghiệm phân biệt
Theo hệ thức Vi – et ta có:
CM
21 tháng 3 2019
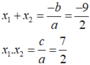
Ta có: ∆ = - 7 2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 =-b/a =7/2 ; x 1 x 2 =c/a =2/2 =1
CM
26 tháng 2 2018
Ta có : ∆ = - 3 2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 = -b/a = 3/(1,4) = 30/14 = 15/7 ; x 1 x 2 = c/a = (1,2)/(1,4) = 12/14 = 6/7
Ta có: Δ = 1 2 -4.5.2 = 1 - 40 = -39 < 0
CM
15 tháng 4 2018
Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
12 tháng 1
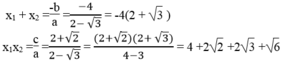
a: Thay m=1 vào phương trình, ta được:
\(x^2-\left(2\cdot1-1\right)x+2\cdot1-4=0\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b: \(\text{Δ}=\left[-\left(2m-1\right)\right]^2-4\cdot1\cdot\left(2m-4\right)\)
\(=\left(2m-1\right)^2-4\left(2m-4\right)\)
\(=4m^2-4m+1-8m+16\)
\(=4m^2-12m+17=4m^2-12m+9+8\)
\(=\left(2m-3\right)^2+8>=8>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(2m-1\right)\right]}{1}=2m-1\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{2m-4}{1}=2m-4\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1-2x_2=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x_2=2m-1-3=2m-4\\x_1+x_2=2m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_2=\dfrac{2}{3}m-\dfrac{4}{3}\\x_1=2m-1-\dfrac{2}{3}m+\dfrac{4}{3}=\dfrac{4}{3}m+\dfrac{1}{3}\end{matrix}\right.\)
\(x_1\cdot x_2=2m-4\)
=>\(\left(\dfrac{2}{3}m-\dfrac{4}{3}\right)\left(\dfrac{4}{3}m+\dfrac{1}{3}\right)=2m-4\)
=>\(\dfrac{1}{9}\left(2m-4\right)\left(4m+1\right)=2m-4\)
=>\(\left(2m-4\right)\left(4m+1\right)=18m-36\)
=>\(\left(m-2\right)\left(8m+2\right)-18\left(m-2\right)=0\)
=>\(\left(m-2\right)\left(8m+2-18\right)=0\)
=>\(\left(m-2\right)\left(8m-16\right)=0\)
=>\(8\left(m-2\right)^2=0\)
=>\(\left(m-2\right)^2=0\)
=>m-2=0
=>m=2(nhận)
c:
\(x_1^2\cdot x_2+x_1\cdot x_2^2+3\left(x_1+x_2\right)=0\)
=>\(x_1x_2\left(x_1+x_2\right)+3\left(x_1+x_2\right)=0\)
=>\(\left(x_1+x_2\right)\left(x_1x_2+3\right)=0\)
=>\(\left(2m-1\right)\left(2m-4+3\right)=0\)
=>\(\left(2m-1\right)^2=0\)
=>2m-1=0
=>2m=1
=>\(m=\dfrac{1}{2}\)
d: \(A=x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(2m-1\right)^2-2\left(2m-4\right)\)
\(=4m^2-4m+1-4m+8\)
\(=4m^2-8m+9\)
\(=4m^2-8m+4+5=\left(2m-2\right)^2+5>=5\forall m\)
Dấu '=' xảy ra khi 2m-2=0
=>2m=2
=>m=1
e: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1\cdot x_2=2m-4\end{matrix}\right.\)
=>\(x_1+x_2-x_1x_2=2m-1-\left(2m-4\right)=2m-1-2m+4=3\)
f: \(\dfrac{1}{x_1}+\dfrac{1}{x_2}>=1\)
=>\(\dfrac{x_1+x_2}{x_1x_2}>=1\)
=>\(\dfrac{2m-1}{2m-4}-1>=0\)
=>\(\dfrac{2m-1-2m+4}{2m-4}>=0\)
=>\(\dfrac{3}{2m-4}>=0\)
=>2m-4>0
=>2m>4
=>m>2
HM
0
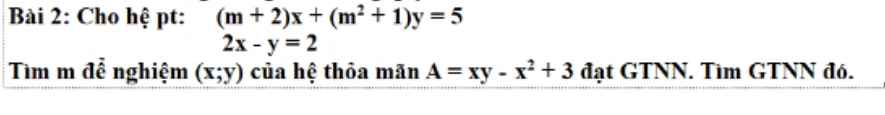
em mới lớp 8
Quá dễ :
Xét 2 trường hợp:
\(\text{*Trường hợp 1 :}\Delta=0\)
Dùng công thức nghiệm rồi tìm tổng và tích các nghiệm là ra ( lưu ý là denta =0 nên có thể dùng bfa'p thế )
\(\text{*Trường hợp 2}:\Delta\ge0\)
tương tự t/h 1
Kết luận ....