Cho tứ giác ABCD. Gọi I, F là trung điểm của BC và CD.Chứng minh :
2(AB→+AI→+FA→+DA→) = 3DB→
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2016
EP // MF (EP là đường trung bình trong ∆BAF) và EP = AF / 2 = MF => MENF là hình bình hành.
=> MP và EF cắt nhau tại trung điểm I.
FN // DE và FN = DE / 2 = QE => FQEN là hình bình hành => QN và EF cắt nhau tại trung điểm I
=> MP và QN cắt nhau tại trung điểm của chúng => MNPQ là hình bình hành
CM
10 tháng 5 2017
Áp dụng tính chất đường trung bình của tam giác ta chứng minh được:
E H = F G = 1 2 B D v à H G = E F = 1 2 A C
Mà AC = BD Þ EH = HG = GF= FE nên EFGH là hình thoi.
30 tháng 7 2023
a) Ta có:-
- M là trung điểm của AB
⇒ AM = MB.
- N là trung điểm của BC
⇒ BN = NC.
- P là trung điểm của CD
⇒ CP = PD.
- Q là trung điểm của DA
⇒ DQ = QA.
Do đó, ta có: AM = MB = BN = NC = CP = PD = DQ = QA.
⇒ tứ giác MNPQ là hình bình hành.
Có:
- I là trung điểm của AC
⇒AI = IC.
- K là trung điểm của BD
⇒ BK = KD.
Do đó, ta có: AI = IC = BK = KD.
⇒ tứ giác INKQ là hình bình hành.
b)Gọi O là giao điểm của MP và NQ ta có:
MP // AB và NQ//CD ( M và N là trung điểm của AB và CD).
⇒ MP song song với NQ.
do đó :O nằm trên MP và NQ.
Gọi H là giao điểm của MI và NK ta có:
MI // AC và NK // BD (do I và K là trung điểm của đường chéo AC và BD).
⇒ MI song song với NK.
Do đó: H nằm trên cả MI và NK.
Gọi G là giao điểm của OH và BD ta có:
OH //MP và BD // MP (do O nằm trên MP và NQ, và H nằm trên MI và NK).
⇒ OH song song với BD.
doo đó: G nằm trên OH và BD.
⇒ I, O, K thẳng hàng.(ĐPCM)
30 tháng 7 2023
a: Xét ΔBAC có BM/BA=BN/BC=1/2
nên MN//AC và MN=1/2AC
Xét ΔDAC có DQ/DA=DP/DC
nên PQ//AC và PQ/AC=DQ/DA=1/2
=>PQ=1/2AC
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔCAB có CI/CA=CN/CB=1/2
nên IN//AB và IN=1/2AB
Xét ΔDAB có DQ/DA=DK/DB=1/2
nên QK//AB và QK=1/2AB
=>IN//QK và IN=QK
=>INKQ là hình bình hành
b: MNPQ là hình bình hành
=>MP cắt NQ tại trung điểm của mỗi đường
=>O là trung điểm của NQ
INKQ là hbh
=>IK cắt NQ tại trung điểm của mỗi đường
=>I,O,K thẳng hàng
3 tháng 1 2024
a:
Ta có: AD//BC
P\(\in\)AD
Do đó: AP//BC
Ta có:BA\(\perp\)AD
P\(\in\)AD
Do đó: BA\(\perp\)PD tại A
Xét ΔMAP vuông tại A và ΔMBC vuông tại B có
MA=MB
\(\widehat{AMP}=\widehat{BMC}\)(hai góc đối đỉnh)
Do đó: ΔMAP=ΔMBC
=>AP=BC
Xét tứ giác APBC có
AP//BC
AP=BC
Do đó: APBC là hình bình hành
Xét tứ giác BCDP có BC//DP
nên BCDP là hình thang
Hình thang BCDP có BC\(\perp\)CD
nên BCDP là hình thang vuông
b: Vì BCDP là hình thang vuông
nên \(S_{BCDP}=\dfrac{1}{2}\left(BC+DP\right)\cdot DC\)
\(=\dfrac{1}{2}\cdot DC\left(BC+DA+AP\right)\)
\(=\dfrac{1}{2}\cdot DC\cdot\left(DC+DC+BC\right)\)
\(=\dfrac{1}{2}\cdot DC\cdot\left(2DC+DC\right)=\dfrac{1}{2}\cdot3DC^2=\dfrac{3}{2}\cdot DC^2\)
Vì AP=BC
mà BC=AD
nên AP=AD
=>A là trung điểm của PD
\(S_{BPAC}=S_{PAB}+S_{ABC}\)
\(=\dfrac{1}{2}\cdot AP\cdot AB+\dfrac{1}{2}\cdot AB\cdot BC\)
\(=\dfrac{1}{2}\cdot BC\cdot AB+\dfrac{1}{2}\cdot BC\cdot AB=BC\cdot AB=AB^2=DC^2\)
=>\(S_{BCDP}=\dfrac{3}{2}\cdot S_{BPAC}\)
=>\(2\cdot S_{BCDP}=3\cdot S_{BPAC}\)
12 tháng 10 2021
a: Xét ΔABD có
E là trung điểm của BA
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//FG và EH=FG
hay EHGF là hình bình hành
18 tháng 4 2022
-Bài hình chẳng ai phụ trách giùm mình hết :v (đặc biệt là hình nâng cao).
-Mình cũng xin lỗi vi tối mới làm đc cho bạn nhé.
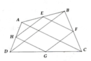
-Gọi E là giao của AD và BC.
\(\widehat{BAE}=180^0-\widehat{BAD}=\widehat{BCD}\)
\(\Rightarrow\)△ABE∼△CDE (g-g).
\(\Rightarrow\dfrac{AE}{CE}=\dfrac{BE}{DE}\Rightarrow\dfrac{AE}{BE}=\dfrac{CE}{DE}\Rightarrow\)△EAC∼△EBD (c-g-c).
\(\Rightarrow\widehat{ICB}=\widehat{IDA}\Rightarrow\)△IBC∼△IAD (g-g)
\(\Rightarrow\dfrac{IB}{IA}=\dfrac{IC}{ID}\Rightarrow\dfrac{IB}{IC}=\dfrac{IA}{ID}\Rightarrow\)△AIB∼△DIC (c-g-c)
\(\Rightarrow\widehat{IAM}=\widehat{IDN};\dfrac{IA}{ID}=\dfrac{AB}{DC}\Rightarrow\dfrac{IA}{ID}=\dfrac{MA}{ND}\Rightarrow\dfrac{IA}{MA}=\dfrac{ID}{ND}\)
\(\Rightarrow\)△AIM∼△DIN (c-g-c) \(\Rightarrow\widehat{AIM}=\widehat{DIN}\)
19 tháng 4 2022
Em cám ơn thầy nhiều lắm ạ!
Em đã hiểu bài rồi thầy ạ! Trân trọng sự giúp đỡ của thầy ạ!
Lời giải:
Ta có:
\(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{FA}+\overrightarrow{DA}=(\overrightarrow{FA}+\overrightarrow{AI})+(\overrightarrow{DA}+\overrightarrow{AB})\)
\(=\overrightarrow{FI}+\overrightarrow{DB}(1)\)
Vì $I,F$ lần lượt là trung điểm của $BC,CD$ nên $FI$ là đường trung bình của tam giác $DBC$
\(\Rightarrow FI\parallel DB, FI=\frac{1}{2}DB\)
\(\Rightarrow \overrightarrow{FI}=\frac{1}{2}\overrightarrow{DB}(2)\)
Từ \((1);(2)\Rightarrow \overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{FA}+\overrightarrow{DA}=\frac{1}{2}\overrightarrow{DB}+\overrightarrow{DB}=\frac{3}{2}\overrightarrow{DB}\)
\(\Rightarrow 2(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{FA}+\overrightarrow{DA})=3\overrightarrow{DB}\) (đpcm)
cho em hỏi sao ra vecto FA + vecto AI vậy ạ