|3-2x| |4y 5|=0

NT

Nguyễn Thị Ngân

17 tháng 9 2021 - olm

|3-2x|+|4y+5|=0

#Hỏi cộng đồng OLM #Toán lớp 7

1

GS

Green sea lit named Wang Junkai

17 tháng 9 2021

$| 3 - 2 x | + | 4 y + 5 | = 0$

$\Rightarrow | 3 - 2 x | = 0$ và $| 4 y + 5 | = 0$

+) $| 3 - 2 x | = 0 \Rightarrow 3 - 2 x = 0 \Rightarrow x = 32$

+) $| 4 y + 5 | = 0 \Rightarrow 4 y + 5 = 0 \Rightarrow y = 54$

Vậy $x = 32; y = 54$

Đúng(0)

NN

No name

4 tháng 8 2019 - olm

|3-2x|+|4y+5|=0

#Hỏi cộng đồng OLM #Toán lớp 6

1

TV

truong vo ki

4 tháng 8 2019

=>3-2x =0 =>$\orbr{\begin{cases}2x=3\\2x=-3\end{cases}}$=>$\orbr{\begin{cases}x=1.5\\x=-1.5\end{cases}}$

=>4y+5=0=>4y=-5=>y=-1.25 Vậy x=1.5 hoặc x=-1.5 , y=-1.25

Đúng(0)

BN

Bảo Nguyễn

27 tháng 10 2021

a)2x+1/2 = 4y-5/9 = 2x+4y-4 /2020x

b)(7y - x)²⁰²⁰+ | 5 - 11x|²⁰²¹= 0

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

27 tháng 10 2021

b: $\Leftrightarrow\left\{{}\begin{matrix}x-7y=0\\11x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{11}\\y=\dfrac{x}{7}=\dfrac{5}{77}\end{matrix}\right.$

Đúng(1)

BN

Bảo Nguyễn

27 tháng 10 2021

a)2x+1/2 = 4y-5/9 = 2x+4y-4 /2020x

b)(7y - x)²⁰²⁰+ | 5 - 11x|²⁰²¹= 0

#Hỏi cộng đồng OLM #Toán lớp 7

2

AH

Akai Haruma

Giáo viên

27 tháng 10 2021

Lời giải:
a. Bạn cần viết đề bằng công thức toán để đề được rõ ràng hơn.

b. Ta có:

$(7y-x)^{2020}\geq 0$ với mọi $x,y$

$|5-11x|^{2021}\geq 0$ với mọi $x,y$

Do đó để tổng của chúng bằng $0$ thì:

$(7y-x)^{2020}=|5-11x|^{2021}=0$

$\Leftrightarrow x=\frac{5}{11}; y=\frac{5}{77}$

Đúng(1)

BN

Bảo Nguyễn

27 tháng 10 2021

Đúng(0)

MN

Mai Nguyễn Bảo Ngọc

15 tháng 6 2017

giải pt

a> x^2+y^2+2x-4y+5=0

b> x^2+4y^2-x-4y+5/4=0

#Hỏi cộng đồng OLM #Toán lớp 8

2

HL

Hà Linh

15 tháng 6 2017

a) x² + y² +2x - 4y + 5 = 0

( x² + 2x + 1 ) + ( y² - 4y + 4 ) = 0

( x + 1 )² + ( y - 2 )² = 0

$\Rightarrow\left\{{}\begin{matrix}x+1=0\\y-2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.$

Đúng(0)

HL

Hà Linh

15 tháng 6 2017

b) $x^2+4y^2-x-4y+\dfrac{5}{4}=0$

$x^2-x+\dfrac{1}{4}+4y^2-4y+1=0$

$\left(x-\dfrac{1}{2}\right)^2+\left(2y-1\right)^2=0$

$\Rightarrow\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\2y-1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.$

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

29 tháng 9 2023

Xét vị trí tương đối của mỗi cặp đường thẳng sau

a) ${d_1}:3x + 2y--5 = 0$ và ${d_2}:x - 4y + 1 = 0$ ;

b) ${d_3}:x - 2y + 3 = 0$ và ${d_4}: - {\rm{ }}2x + 4y + 10 = 0$ ;

c) ${d_5}:4x + 2y - 3 = 0$ và ${d_6}:\left\{ \begin{array}{l}x = - \frac{1}{2} + t\\y = \frac{5}{2} - 2t\end{array} \right.$

#Hỏi cộng đồng OLM #Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

29 tháng 9 2023

a) Tọa độ giao điểm của hai đường thẳng ${d_1},{d_2}$ là nghiệm của hệ phương trình:

$\left\{ \begin{array}{l}3x + 2y - 5 = 0\\x - 4y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{9}{7}\\y = \frac{4}{7}\end{array} \right.$

Hệ phương trình có nghiệm duy nhất nên 2 đường thẳng cắt nhau.

b) Tọa độ giao điểm của hai đường thẳng ${d_3},{d_4}$ là nghiệm của hệ phương trình:

$\left\{ \begin{array}{l}x - 2y + 3 = 0\\ - 2x + 4y + 10 = 0\end{array} \right.$ .

Hệ phương trình vô nghiệm.nên 2 đường thẳng song song với nhau

c) Tọa độ giao điểm của hai đường thẳng ${d_5},{d_6}$ tương ứng với t thỏa mãn phương trình:

$4\left( { - \frac{1}{2} + t} \right) + 2\left( {\frac{5}{2} - 2t} \right) - 3 = 0 \Leftrightarrow 0t = 0$ .

Phương trình này có nghiệm với mọi t. Do đó ${d_5} \equiv {d_6}$.

Đúng(0)

LT

Lan Triệu

3 tháng 2 2021

|x+25|+|−y+5|=0⇒|x+25|=0 và |−y+5|=0+) |x+25|=0⇒x+25=0⇒x=−25+) |−y+5|=0⇒−y+5=0⇒−y=−5⇒y=5Vậy cặp số (x;y) là (−25;5) Những câu b-f thì chia ra làm 2 vế rồi tínhg thì tìm ước rồi lập bảng trường hợp trong ước h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ta có một...

Đọc tiếp

|x+25|+|−y+5|=0

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

(4y−2)=2(2y−1)(4y−2)=2(2y−1)

⇒|x+25|=0 và |−y+5|=0

+) |x+25|=0

⇒x+25=0

⇒x=−25

+) |−y+5|=0

⇒−y+5=0

⇒−y=−5

⇒y=5

Vậy cặp số (x;y) là (−25;5)

Những câu b-f thì chia ra làm 2 vế rồi tính

g thì tìm ước rồi lập bảng trường hợp trong ước

h. (2x−1).(4y−2)=−42(2x−1).(4y−2)=−42

⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)⇒{2x−1∈Ư(−42)4y−2∈Ư(−42)

Mà: Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}Ư(−42)∈{±1;±2;±3;±6;±7;±21;±42}

Ta có một số trường hợp sau :

2x−12x−1	1	-1	2	-2	3	-3
(4y−2)=2(2y−1)(4y−2)=2(2y−1)	-1	1	-2	2	-

#Hỏi cộng đồng OLM #Toán lớp 6

2

PT

Phong Thần

3 tháng 2 2021

nó khó nhìn thiệt ha

Đúng(1)

PT

Phong Thần

3 tháng 2 2021

định châm chọc mình làm khó coi à

mình có bt đâu tự nhiên nó thế

ai mà bt đc giờ

Đúng(0)

PT

Pham Trong Bach

7 tháng 2 2018

Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:

d1: -3x + 6y – 3 = 0;

d2: y = -2x;

d3: 2x + 5 = 4y.

#Hỏi cộng đồng OLM #Toán lớp 10

1

CM

Cao Minh Tâm

7 tháng 2 2018

Xét Δ và d1, hệ phương trình: 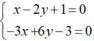Giải bài tập Toán 10 | Giải Toán lớp 10 có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.

Xét Δ và d2, hệ phương trình: 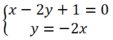Giải bài tập Toán 10 | Giải Toán lớp 10 có nghiệm duy nhất (-1/5; 2/5) nên

Δ cắt d2 tại điểm M(-1/5; 2/5).

Xét Δ và d3, hệ phương trình: 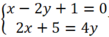Giải bài tập Toán 10 | Giải Toán lớp 10 vô nghiệm

Vậy Δ // d3

Đúng(0)

NM

nam mai

3 tháng 8 2019 - olm

Tìm x:

$x^3-x^2=4x^2-8x+4\\ $

$x^4+2x^3-4x-4=0$

$2x^2+z^2+4y-x+2xz+4y^2+\frac{5}{4}=0$

#Hỏi cộng đồng OLM #Toán lớp 8

1

K

KAl(SO4)2·12H2O

3 tháng 8 2019

1) $x^3-x^2=4x^2-8x+4$

$\Leftrightarrow x^3-x^2-4x^2+8x-4=0$

$\Leftrightarrow x^2-5x^2+8x-4=0$

$\Leftrightarrow\left(x^2-4x+4\right)\left(x-1\right)=0$

$\Leftrightarrow\left(x^2-2x.2+2^2\right)\left(x-1\right)=0$

$\Leftrightarrow\left(x-2\right)^2\left(x-1\right)=0$

$\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=1\end{cases}}$

$\Rightarrow\orbr{\begin{cases}x=1\\x=2\end{cases}}$

Đúng(0)

PN

Phạm Nguyệt

20 tháng 6 2016 - olm

1. Tìm giá trị của x để :

a. x²+ 5x < 0

b. 3(2x + 3) (3x - 5) < 0

2. Tìm giá trị của y để :

a. 2y² - 4y > 0

b. 5(3y + 1) (4y - 3) > 0

#Hỏi cộng đồng OLM #Toán lớp 7

1

NH

Nguyễn Hoàng Tiến

20 tháng 6 2016

a) $X^2+5X< 0$

<=> $X\left(X+5\right)< 0$

<=> TH1: $x< 0;x+5>0\Leftrightarrow-5< x< 0$

TH2: $x>0;x+5< 0\Leftrightarrow0< x< -5$ (vô lí)

Vậy $-5< x< 0$

Đúng(0)

NL

nguyen lan phuong

21 tháng 12 2015 - olm

bài 2 tìm x, y sao cho

a /3-2x/+/4y+5/=0

b /5x-3/+/2y-7/=0

#Hỏi cộng đồng OLM #Toán lớp 7

1

VT

Vương Thị Diễm Quỳnh

21 tháng 12 2015

a/ l 3-2xl + l 4y+5 l =0

mà l 3-2x l $\ge$0

l 4y+5 l $\ge$0

=>l 3-2x l =0 và l 4y+5 l = 0

=>3-2x=0 và 4y+5=0

=>x=3/2 và y= -5/4

b/l 5x-3l +l2y-7l=0

mà ..

=>.. tự làm nhé

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP