Giúp e chi tiết câu 1,2,3,5 vs ạ.E cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)ABE = 180 độ - 35 độ = 145 độ
b) Vì DBC + BCy = 180 độ
=>Cy // DE
mà DE // Ax
=>Ax//Cy

1.
\(cos\left(\dfrac{2\pi}{3}+2x\right)+cos\left(\dfrac{\pi}{3}+x\right)+1=0\)
\(\Leftrightarrow2cos^2\left(\dfrac{\pi}{3}+x\right)+cos\left(\dfrac{\pi}{3}+x\right)=0\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{3}+x\right)\left[2cos\left(\dfrac{\pi}{3}+x\right)+1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(\dfrac{\pi}{3}+x\right)=0\\cos\left(\dfrac{\pi}{3}+x\right)=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}+x=\dfrac{\pi}{2}+k\pi\\\dfrac{\pi}{3}+x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)

40: Ta có: \(A=27x^3+8y^3-3x-2y\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)-\left(3x+2y\right)\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2-1\right)\)

\(\lim\limits_{x\rightarrow5}\left(x^3+5x^2-10x+8\right)=5^3+5.5^2-10.5+8=...\)
\(\lim\limits_{x\rightarrow-2}\dfrac{x^3-x^2-2x-8}{x^2+3x+2}=\dfrac{-16}{0}=-\infty\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x^2-5x+2}{2\left|x\right|+1}=\lim\dfrac{\left|x\right|-5+\dfrac{2}{\left|x\right|}}{2+\dfrac{1}{\left|x\right|}}=\dfrac{+\infty}{2}=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt[3]{x^3+4x-3}-4x}{\sqrt{9x^2-5x+1}-4x}=\lim\limits_{x\rightarrow+\infty}\dfrac{x\left(\sqrt[3]{1+\dfrac{4}{x^2}-\dfrac{3}{x^3}}-4\right)}{x\left(\sqrt[]{9-\dfrac{5}{x}+\dfrac{1}{x^2}}-4\right)}=\dfrac{1-4}{3-4}=3\)
Lời giải:
a.
\(\lim\limits_{x\to 5}(x^3+5x^2-10x+8)=5^3+5.5^2-10.5+8=208\)
b.
\(L=\lim\limits_{x\to -2}\frac{x^3-x^2-2x-8}{x^2+3x+2}\lim\limits_{x\to -2}\frac{x^3-x^2-2x-8}{x+1}.\frac{1}{x+2}=16\lim\limits_{x\to -2}\frac{1}{x+2}\)\(\lim\limits_{x\to -2-}\frac{1}{x+2}=-\infty \Rightarrow L=-\infty ; \lim\limits_{x\to -2+}\frac{1}{x+2}=+\infty \Rightarrow L=+\infty \)




a.
Đặt \(sinx+cosx=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(2t+t^2-1+1=0\)
\(\Rightarrow t\left(t+2\right)=0\Rightarrow\left[{}\begin{matrix}t=0\\t=-2< -\sqrt{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=0\)
\(\Rightarrow tanx=-1\)
\(\Rightarrow x=-\dfrac{\pi}{4}+k\pi\)
a, Đặt \(sinx+cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(pt\Leftrightarrow2t+t^2-1+1=0\)
\(\Leftrightarrow t^2+2t=0\)
\(\Leftrightarrow t\left(t+2\right)=0\)
\(\Leftrightarrow t=0\)
\(\Leftrightarrow sinx+cosx=0\)
\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\)




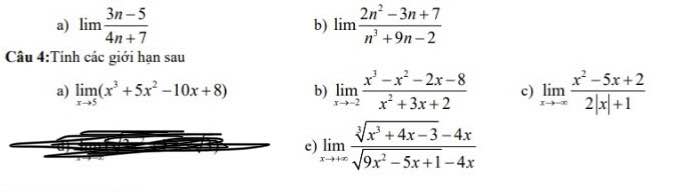





 viết tiếp bức thư ạ.nhannh giúp e vs ạ.e cảm ơn
viết tiếp bức thư ạ.nhannh giúp e vs ạ.e cảm ơn

1. Hàm \(y=cos\left(3x+\dfrac{\pi}{3}\right)\) có chu kì \(T=\dfrac{2\pi}{\left|3\right|}=\dfrac{2\pi}{3}\)
2. \(y=4sin2x.cos3x=2sin5x-2sinx\)
Hàm \(y=2sin5x\) có chu kì \(T_1=\dfrac{2\pi}{5}\)
Hàm \(y=2sinx\) có chu kì \(T_2=2\pi\)
\(\Rightarrow y=2sin5x-2sinx\) có chu kì \(T=BCNN\left(\dfrac{2\pi}{5};2\pi\right)=2\pi\)
3.
Hàm \(y=cot\left(x+\dfrac{\pi}{4}\right)\) có chu kì \(T=\pi\)
5.
Hàm \(y=tan\left(\dfrac{\pi}{3}+\dfrac{x}{5}\right)\) có chu kì \(T=\dfrac{\pi}{\left|\dfrac{1}{5}\right|}=5\pi\)