Cho 1 tứ giác PSRQ , có S=65 độ , R = 95 độ . Tính P, Q , gọi P, Q là x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
30 tháng 8 2018
Theo tính chất hình bình hành ta luôn có hai góc đối diện luôn bằng nhau .
Do đó : \(\widehat{P}=\widehat{R}=95^0\) và \(\widehat{Q}=\widehat{S}=65^0\)
TP
1
OP
4 tháng 8 2016
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
A + 950 = 1800
A = 1800 - 950
A = 850
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
B + 650 = 1800
B = 1800 - 650
B = 1150
CM
5 tháng 8 2018
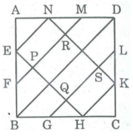
Diện tích hình vuông ABCD bằng 6.6 = 36 ( c m 2 )
Diện tích △ BEH bằng 1/2 .4.4 = 8 ( c m 2 )
Diện tích △ DKN bằng 1/2 .4.4 = 8 ( c m 2 )
Diện tích phần còn lại là: 36 - (8 + 8) = 20 ( c m 2 )
Trong tam giác vuông AEN, ta có:
E N 2 = A N 2 + A E 2 = 4 + 4 = 8 ⇒ EN = 2 2 (cm)
Trong tam giác vuông BHE, ta có:
E H 2 = B E 2 + B H 2 = 16 + 16 = 32 ⇒ EH = 4 2 (cm)
Diện tích hình chữ nhật ENKH bằng: 2 2 . 4 2 = 16 ( c m 2 )
Nối đường chéo BD. Theo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH được chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 c m 2
Diện tích △ AEN bằng 1/2 .2.2 = 2 ( c m 2 )
Vậy S A E P S N = S A E N + S E P S N = 2 + 16/4 = 6 ( c m 2 )
CM
31 tháng 7 2019
1) Ta có:
• PQ là đường trung bình của ΔABC nên PQ // BC và PQ = BC/2 (1)
• RS là đường trung bình của ΔDBC nên RS // BC và RS = BC/2 (2)
Từ (1) và (2) suy ra PQ // RS và PQ = RS
Suy ra tứ giác PQRS là hình bình hành.
CM
28 tháng 4 2017
Đáp án A
Ký hiệu như hình vẽ. Đặt A B = B C = C D = D A = a ; S O = h
Suy ra S B = a 2 2 + h 2
Gọi M là trung điểm của SB
Trong (SBD) kẻ trung trực của SB cắt SO tại I
Vậy I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD. Suy ra I S = R .
Hai tam giác vuông SMI và SOB đồng dạng ⇒ S I S B = S M S O ⇒ R = a 2 + 2 h 2 4 h với 0 < h < 2 R . Suy ra a 2 = 2 h 2 R − h .
Thể tích V của khối chóp là:
V = 1 3 a 2 h = 1 3 2 h 2 2 R − h = 8 3 h 2 h 2 2 R − h ≤ 8 3 h 2 + h 2 + 2 R − h 3 3 = 64 R 3 81
Vậy GTLN của V bằng 64 R 3 81 đạt được khi h 2 = 2 R − h ⇔ h = 4 R 3
Suy ra a = 4 R 3 .
. Gọi M, N, P, Q theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.
10 tháng 12 2021
b: Xét ΔABC có
M là trung điểm của BA
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành