GIÚP GIẢI CHI TIẾT VỚI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.I think you ought to give up playing video games. (should)
-->I think you should give up playing video games.
2.It's necessary for me to finish the work on time. (have to)
--->I have to finish the work on time.
3.It wasn't necessary for you to clean that car. (have to)
--->You didn't have to clean that car.
4.It was quite unnecessary for you to adopt a green lifestyle. (have to)
---->You didn't have to adopt a green lifestyle.
5.It was careless of you to leave the windows open last night. (shouldn't)
----->You shouldn't have left the windows open last night.
6.It is advisable for each member in the family to share the housework equally. (should)
---->Each member in the family should share the housework equally.
7.You are required to come back home before 10 p.m. (must)
--->You must come back home before 10 p.m.
8.Lina is advised to prepare carefully in the morning. (should)
----->Lina should prepare carefully in the morning.
9.Tu is responsible for picking up litter. (have to)
------>Tu has to pick up litter.
1.You are required to ask your parents for permission before staying out late. (must)
You must ask your parents for permission before staying out late.
2.I think you ought to give up smoking immediately. (should)
I think you should give up smoking immediately.
3.It is not a good idea for me to stay up late. (shouldn't)
I shouldn't stay up late.
4.It wasn't necessary for you to send these letters. (have to)
You didn't have to send these letters.
5.It was unnecessary for Tim to finish the work. (have to)
Tim didn't have to finish the work.
6.It was careless of you to leave your children alone at home. (shouldn't)
You shouldn't have left your children alone at home.
Bằng 1 cách nào đó 1 câu hỏi từ 2023 ở đây và tôi vẫn trả lời nó sau 1 năm :v

10B
x=A*cos(\(\omega t+\varphi\))
x=5*cos(\(\omega t\))
=>A=5
11A:
Biên độ dao động bằng quỹ đạo chia đôi
=>A=MN/2=15cm
12C
\(y=-10\cdot cos\left(4\Pi t-\dfrac{pi}{4}\right)=10\cdot cos\left(4\Pi t+\dfrac{pi}{4}\right)\)
=>Pha dao động ban đầu là pi/4
13C
\(y=-8cos\left(2t+\dfrac{pi}{2}\right)=8\cdot\left[-cos\left(2t+\dfrac{pi}{2}\right)\right]\)
\(=8\cdot cos\left(2t-\dfrac{pi}{2}\right)\)
=>Pha dao động ban đầu là -pi/2

a.
Công thức góc cơ bản: \(cos\left(a+k\pi\right)=\pm cosa\) ; \(sin\left(a+k2\pi\right)=sina\) ; \(cos\left(a+\dfrac{\pi}{2}\right)=-sina\)
Do đó pt tương đương:
\(2cosx+\dfrac{1}{3}cos^2x=\dfrac{8}{3}+sin2x-3sinx+\dfrac{1}{3}sin^2x\)
\(\Leftrightarrow6cosx+1-sin^2x=8+3sin2x-9sinx+sin^2x\)
\(\Leftrightarrow2sin^2x-9sinx+7+6sinx.cosx-6cosx=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx-7\right)+6cosx\left(sinx-1\right)=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx+6cosx-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\\2sinx+6cosx=7\left(1\right)\end{matrix}\right.\)
Xét (1), ta có \(2^2+6^2=40< 7^2\) nên (1) vô nghiệm
Vậy họ nghiệm của pt là \(x=\dfrac{\pi}{2}+k2\pi\)
b.
Ta có:
\(tan^2x\left(1-sin^3x\right)+cos^3x-1=0\)
\(\Leftrightarrow\dfrac{\left(1-cos^2x\right)\left(1-sin^3x\right)}{\left(1-sin^2x\right)}-\left(1-cos^3x\right)=0\)
\(\Leftrightarrow\dfrac{\left(1-cosx\right)\left(1+cosx\right)\left(1+sinx+sin^2x\right)}{1+sinx}-\left(1-cosx\right)\left(1+cosx+cos^2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\Rightarrow x=k2\pi\\\dfrac{\left(1+cosx\right)\left(1+sinx+sin^2x\right)}{1+sinx}=1+cosx+cos^2x\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Rightarrow\left(1+cosx\right)\left(1+sinx+sin^2x\right)=\left(1+sinx\right)\left(1+cosx+cos^2x\right)\)
\(\Leftrightarrow sin^2x+sin^2x.cosx=cos^2x+cos^2x.sinx\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\Rightarrow x=\dfrac{\pi}{4}+k\pi\\sinx+cosx+sinx.cosx=0\left(2\right)\end{matrix}\right.\)
Xét (2), đặt \(sinx+cosx=t\Rightarrow\left|t\right|\le\sqrt{2}\)
\(sinx.cosx=\dfrac{t^2-1}{2}\)
Pt (2) trở thành:
\(t+\dfrac{t^2-1}{2}=0\Leftrightarrow t^2+2t-1=0\Rightarrow\left[{}\begin{matrix}t=-1+\sqrt{2}\\t=-1-\sqrt{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}-1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}-1}{\sqrt{2}}\)
\(\Rightarrow...\)


f) Ta có: \(F=\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\left(\sqrt{6}+11\right)\)
\(=\left(\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{2}-\dfrac{12\left(3+\sqrt{6}\right)}{3}\right)\left(\sqrt{6}+11\right)\)
\(=\left[3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)\right]\cdot\left(11+\sqrt{6}\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(11+\sqrt{6}\right)\)
\(=\left(\sqrt{6}-11\right)\left(11+\sqrt{6}\right)\)
=6-121=-115

câu 1 là 2 cạnh góc vuông hay 1 cạnh góc vuông và cạnh huyền thế
câu 2 AC là cạnh góc vuông hay cạnh huyền
1. Xét \(\Delta\)ABC vuông tại A, theo tỉ số lượng giác ta có
\(\cos B=\dfrac{AB}{BC}=\dfrac{6}{10}\Rightarrow B=53^O\\ C=A-B=90^o-53^o=37^o\\ AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8\)
2. Xét \(\Delta\)ABC vuông tại A, theo tỉ số lượng giác ta có
\(\sin C=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{\sin C}=\dfrac{5}{sin30}=10\\ AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-5^2}=5\sqrt{3}\\ B=A-C=90^o-30^o=60^o\)


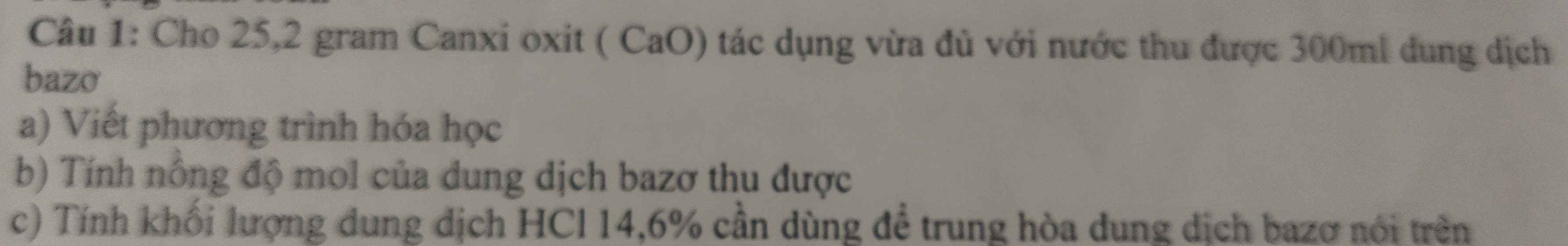

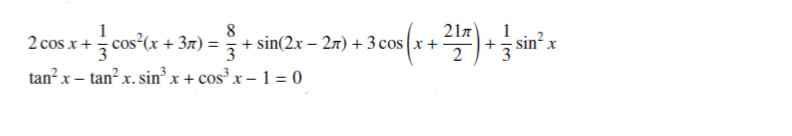

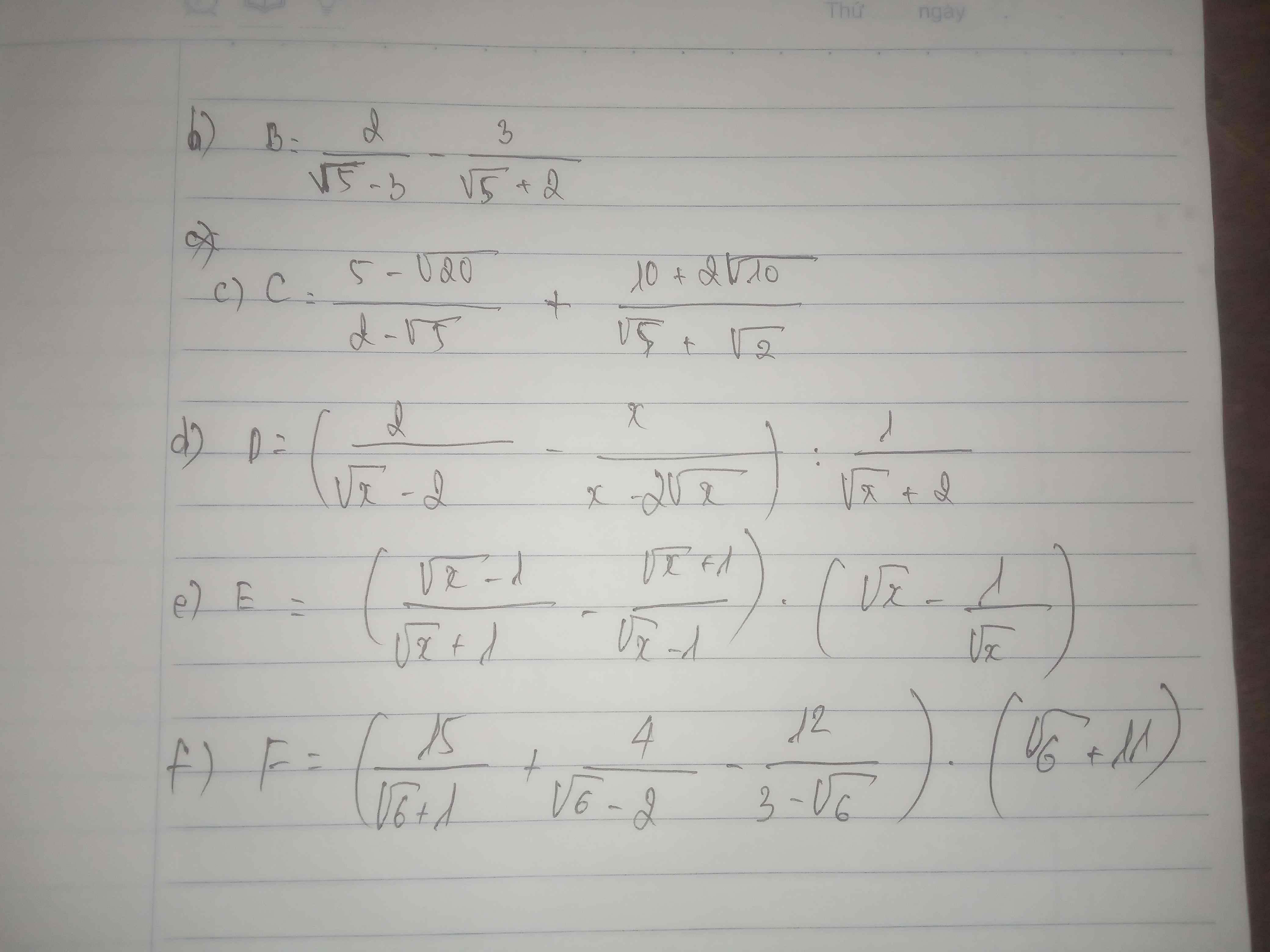
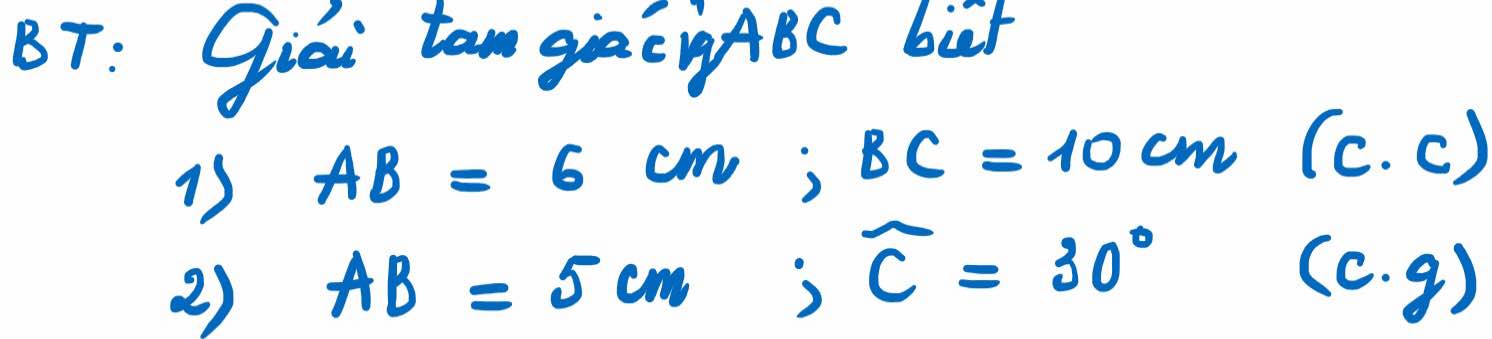

S A B C D
Do SA = 3AB = 2AD => \(\hept{\begin{cases}AD=\frac{SA}{2}\\AB=\frac{SA}{3}\end{cases}}\)
thể tích hình chóp bằng 6 => \(6=\frac{1}{3}SA.AD.AB=\frac{1}{3}.\frac{SA^3}{6}=\frac{SA^3}{18}\)
(do đáy là hcn lên Sđáy = AD.AB)
=> SA3 = 108 =>SA = \(\sqrt[3]{108}\)
=> Sđáy = \(18\sqrt[3]{108}\)