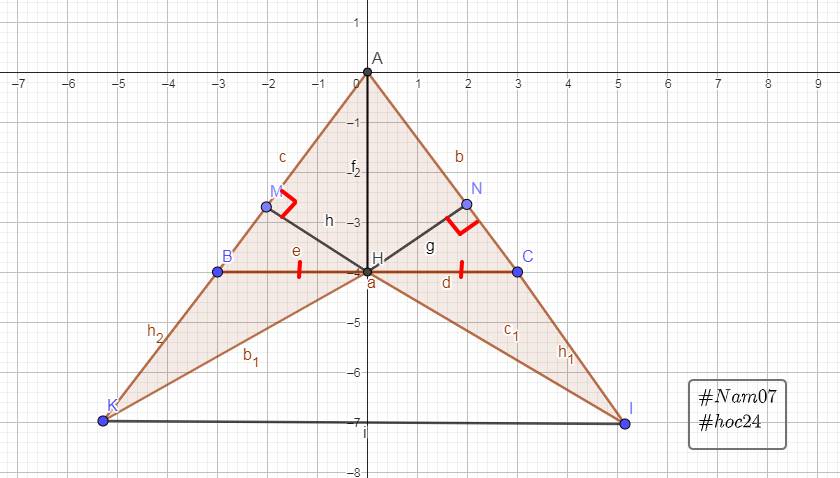
Cho tam giac ABC nhọn BM,CN cắt nhau tại K
a, tam giác AKN ~BKM
b,tam giác AKB~NKM
c,kẻ MH vuông góc AC c/m MH^2=AC×HC
d,gọi I là giao điểm của KH và MN Kẻ IE vuông góc AC
Gọi F là giao điểm của IE và KM c/m 1/KM +1/MH=2/EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2023
`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.
28 tháng 3 2021
a) Xét ΔABI vuông tại A và ΔEBI vuông tại E có
BI chung
\(\widehat{ABI}=\widehat{EBI}\)(BI là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABI=ΔEBI(Cạnh huyền-góc nhọn)
Suy ra: AI=EI(hai cạnh tương ứng)
9 tháng 2 2019
a) Xét \(\Delta AHB\)và\(\Delta AHC\)có :
\(\hept{\begin{cases}HB=HC\\AH\\AB=AC\end{cases}}\)( Bạn tự ghi lời giải thích nha)
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}\)(2 cạnh tương ứng)
Mà \(\widehat{AHB}+\widehat{AHC}=180^o\)( 2 góc kề bù )
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AH\perp BC\)
b) Xét \(\Delta AHM\left(\widehat{AMH}=90^o\right)\)và \(\Delta AHN\left(\widehat{ANH}=90^o\right)\)có :
\(\hept{\begin{cases}AH\\\widehat{A_1}=\widehat{A_2}\end{cases}}\)( bạn tự nêu lí do )
\(\Rightarrow\Delta AHM=\Delta AHN\)( Cạnh huyền - góc nhọn )
DT
26 tháng 4 2019
a, xét 2 tam giác vuông ABM và HBM có:
MB cạnh chung
\(\widehat{ABM}\)=\(\widehat{HBM}\)(gt)
=> \(\Delta\)ABM=\(\Delta\)HBM (CH-GN)
b, Vì \(\Delta\)ABM=\(\Delta\)HBM(câu a) suy ra MA=MH(2 cạnh tương ứng)
c,Ta có: \(\Delta\)AMK=\(\Delta\)HMC(cạnh góc vuông-góc nhọn kề)
=> AK=HC(2 cạnh tương ứng) mà AB=HB suy ra KB=CB
=> \(\Delta\)KBC cân tại B
8 tháng 3 2023
â: Xét ΔBAI vuông tại A và ΔBEI vuông tại E có
BI chung
góc ABI=góc EBI
=>ΔBAI=ΔBEI
=>IA=IE
mà IE<IC
nên IA<IC
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc B chung
=>ΔBEF=ΔBAC
=>BF=BC
mà BI là phân giác
nên BI vuông góc CF
2 tháng 3 2022
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM vừa là đường cao vừa là đường phân giác
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
b: Ta có: ΔAHK cân tại A
mà AM là đường phân giác
nên AM là đường trung trực của HK
BM, CN là gì ( là đuờng cao hay gì )
Viết đề hài