rút gọn biểu thức:12+22+32+............+20182
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
26 tháng 11 2021
ghi cả cách giải nữa chứ,ghi mỗi đáp án thì làm sao hiểu được
NT
2
NT
27 tháng 4 2021
a.Chứng tỏ rằng B = 1/22 + 1/32 + 1/42 + 1/52 + 1/62 + 1/72 +1/82 < 1
b.Cho S = 3/1.4 + 3/4.7 + 3/7.10 +......+3/40.43 + 3/43.46 hãy chứng tỏ rằng S < 1
NT
27 tháng 4 2021
Xin lỗi mọi người mình tính đặt câu hỏi nhưng ấn nhầm phần trả lời ạ!
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
21 tháng 7 2023
a, A = 1002 - 992 + 982 - 972 +...+ 22 - 12
A = (1002 - 992) + (982 - 972) +...+ (22 - 1)2
A = (100 - 99)(100+99) + (98-97)(98+97)+..+(2-1)(2+1)
A = 1.199 + 1.195 + 1.191 +...+1.3
A = 3 + ...+191+ 195 + 199
Dãy số trên là dãy số cách đều với khoảng cách là: 199 -195=4
Dãy số trên có số hạng là: (199 - 3): 4 + 1 = 50 (số )
A = (199 +3) \(\times\) 50 : 2 = 5050
C
3
H
3 tháng 7 2021
a) \(153^2-53^2=\left(153-53\right)\left(153+53\right)=100.206=20600\)
b)
\(\left(2020^2-2019^2\right)+\left(2018^2-2017^2\right)+...+\left(2^2-1^2\right)\\ =\left(2020+2019\right)\left(2020-2019\right)+\left(2018+2017\right)\left(2018-2017\right)+...+\left(2+1\right)\left(2-1\right)\\ =2020+2019+2018+2017+...+2+1\\ =\dfrac{\left(2020+1\right)2020}{2}=2041210\)
AH
Akai Haruma
Giáo viên
3 tháng 7 2021
Lời giải:
a. $153^2-53^2=(153-53)(153+53)=100.206=20600$
b.
$2020^2-2019^2+2018^2-2017^2+...+2^2-1^2$
$=(2020^2-2019^2)+(2018^2-2017^2)+...+(2^2-1^2)$
$=(2020-2019)(2020+2019)+(2018-2017)(2018+2017)+...+(2-1)(2+1)$
$=2020+2019+2018+2017+...+2+1$
$=\frac{2020.2021}{2}=2041210$
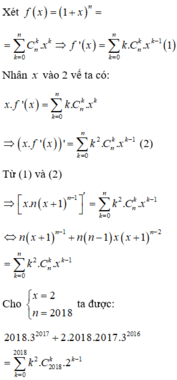
Đặt \(D=1^2+2^2+3^2+...+2018^2\)
\(D=1\left(2-1\right)+2\left(3-1\right)+3\left(4-1\right)+...+2018\left(2019-1\right)\)
\(D=1.2-1+2.3-2+3.4-3+...+2018.2019-2018\)
\(D=\left(1.2+2.3+...+2018.2019\right)-\left(1+2+3+...+2018\right)\)
Đặt \(A=1.2+2.3+...+2018.2019\)
\(\Rightarrow3A=1.2.3+2.3.\left(4-1\right)+...+2018.2019\left(2020-2017\right)\)
\(\Rightarrow3A=2018.2019.2010\Rightarrow A=\frac{2018.2019.2020}{3}\)
Đặt \(B=1+2+3+...+2018\)
\(B=\frac{\left(2018+1\right)\left(2018-1+1\right)}{2}=\frac{2019.2018}{2}\)
\(\Rightarrow D=A+B=\frac{2018.2019.2020}{3}+\frac{2019.2018}{2}\)
\(\Rightarrow D=\frac{2018.2019.2020.2+2019.2018.3}{6}\)