Cho hình chữ nhật ABCD và O nằm trong hình chữ nhật đó
CMR: OA2 + OC2 = OB2 + OD2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 7 2019
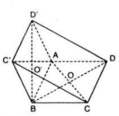
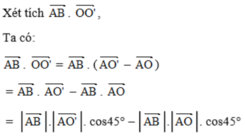
+) Vì hai hình vuông ABCD và ABC’D’ có cùng độ dài cạnh là AB
nên hai đường chéo bằng nhau: AC = AC’.
Suy ra: AO = AO’ hay |AO'→| = |AO→| .
Suy ra: AB→.OO'→ = 0 ⇒ AB ⊥ OO'
CM
1 tháng 5 2018
Đáp án B
Lưới hình vuông ở trên được tạo thành bởi 7 đường kẻ dọc và 5 đường kẻ ngang. Với mỗi cách chọn hai đường kẻ ngang và hai đường kẻ dọc ta thu được đúng một hình chữ nhật với các đỉnh là giao điểm của các đường đó. Từ đó suy ra số hình chữ nhật cần tìm là:
C 7 2 . C 5 2 = 210 .
CM
14 tháng 1 2018
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.
Gọi N và Q là hình chiếu của O trên AD, BC
Áp dụng Pytago ta có:
OA2 = AN2 + ON2
OC2= OQ2 + QC2
suy ra: OA2 + OC2 = AN2 + ON2 + OQ2 + QC2
= (BQ2 + QB2) + (ON2 + ND2)
= OB2 + OD2
Gọi N và Q là hình chiếu của O trên AD, BC
Áp dụng Pytago ta có:
OA2 = AN2 + ON2
OC2= OQ2 + QC2
suy ra: OA2 + OC2 = AN2 + ON2 + OQ2 + QC2
= (BQ2 + QB2) + (ON2 + ND2)
= OB2 + OD2