2 bến sông a và b ở bên 1 con sông nước chảy. Một ca nô đi từ a đến b rồi quay ngay trở lại từ b đến a mất 5 giờ 15 phút. Vận tốc của ca nô khi đứng yên 5m/s ,khoảng cách giữa hai bên sông a và b là 54km .Hãy tính vận tốc của dòng sông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 10 2016
2h30ph=150ph
3h45ph=225ph
1m/s=60m/ ph
song chay theo huong tu A đến B
khi đi từ A đến B
V1 = V cano + V nuoc = V cano +60
S= V1* t1 = (V cano +60)* 150=150* V cano+ 9000 (m) (1)
khi đi từ B đến A
V2 = V cano - V nuoc = V cano -60
S= V2* t2 = (V cano -60)* 225=225* V cano - 13500 (m) (2)
Tu (1) , (2)
150* V cano+ 9000= 225* V cano – 13500
Suy ra V cano = 300m/ phut
S= 150* V cano+ 9000= 300* 150 +9000=54000m=54km
8 tháng 5 2017
gọi x (Km/ h)là vận tốc của ca nô khi nước yên lặng
vận tốc khi đi suôi dòng là x + 3
vận tốc khi đi ngực dòng là x - 3
thời gian khi đi suôi dòng là \(\dfrac{30}{x+3}\)
thời gian khi đi ngực dòng là \(\dfrac{30}{x-3}\)
thời gian nghỉ là 40 phút = \(\dfrac{40}{60}\) = \(\dfrac{2}{3}\) giờ
vì tổng thời gian từ lúc đi đến lúc trở về là 6 giờ
nên ta có phương trình :
\(\dfrac{30}{x+3}\)+\(\dfrac{30}{x-3}\)+\(\dfrac{2}{3}\) = 6
\(\Leftrightarrow\) \(\dfrac{30.\left(x-3\right)+30.\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}\) +\(\dfrac{2}{3}\) = 6
\(\Leftrightarrow\) \(\dfrac{60x}{x^2-9}\)+\(\dfrac{2}{3}\) = 6\(\Leftrightarrow\) \(\dfrac{60x}{x^2-9}\)= \(\dfrac{16}{3}\)
\(\Leftrightarrow\) 180x = 16x2 - 144\(\Leftrightarrow\) 16x2 -180x -144 = 0
\(\Leftrightarrow\) 4x2 - 45x -36 = 0
giải \(\Delta\) ta có 2 nghiệm :x1=12 (tmđk) ; x2=-\(\dfrac{3}{4}\) (loại)
vậy vận tốc khi nước yên lặng là 12(Km/h)
CM
15 tháng 7 2019
Gọi x (km/h) là vận tốc của ca nô khi nước yên lặng.
Điều kiện: x > 3
Khi đó vận tốc khi đi xuôi dòng trên sông là x + 3 (km/h)
vận tốc khi đi ngược dòng trên sông là x – 3 (km/h)
thời gian ca nô đi xuôi dòng là 30/(x + 3) (giờ)
thời gian ca nô đi ngược dòng là 30/(x - 3) (giờ)
thời gian ca nô nghỉ ở B là 40 phút = 2/3 (giờ)
Theo đề bài, ta có phương trình:
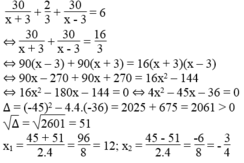
Giá trị x = - 3/4 không thỏa mãn điều kiện bài toán.
Vậy vận tốc của ca nô khi nước yên lặng là 12 km/h.
14 tháng 8 2023
2:
Gọi thời gian dự định là x(h)
Độ dài quãng đường khi đi với vận tốc 45km/h là:
\(45\left(x+\dfrac{1}{2}\right)\)
Độ dài quãng đường khi đi với vận tốc 60km/h là:
\(60\left(x-\dfrac{1}{2}\right)\)
Do đó, ta có phương trình:
45(x+1/2)=60(x-1/2)
=>3(x+1/2)=4(x-1/2)
=>4x-2=3x+1,5
=>x=3,5
ĐỘ dài AB là:
45(3,5+0,5)=45*4=180(km)
