Cho \(\widehat{xOy}\). Vẽ tia Oa là tia phân giác của \(\widehat{xOy}\), tia Ob là tia phân giác \(\widehat{xOa}\), tia Oc là tia phân giác \(\widehat{xOb}\).
a, Tính \(\widehat{xOc}\)nếu \(\widehat{xOy}\)= 90o .
b, Tính GTLN của \(\widehat{xOc}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{xOA}=\widehat{cOA}\) (gt) (1)
\(\widehat{yOB}=\widehat{COB}\) (gt) (2)
\(\widehat{COA}+\widehat{COB}=\widehat{AOB}=90^o\) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{xOA}+\widehat{yOB}=90^o\)
\(\Rightarrow\widehat{xOy}=\widehat{COA}+\widehat{COB}+\widehat{xOA}+\widehat{yOB}=90^o+90^o=180^o\)
=> Ox và Oy là hai tia đối nhau

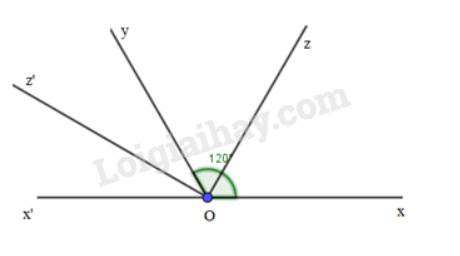
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau

`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`

do Oa là tia phân giác của góc xOy=> góc xOa= góc aOy = 70/2 = 35 độ
do Oy' là tia đối của tia Oy => góc xOy'+góc xOy = 180 độ => góc xOy' = 180-70 = 110
Do Ob tia đối của Oa => góc bOy' + góc y'Oa = 180 độ => góc bOy' + góc y'Ox+ góc xOa = 180 độ
=> góc bOy' + 110 độ + 35 độ =180 độ => góc bOy' = 35 độ
mà góc y'Ox' = góc xOy = 70 độ ( vì đối đỉnh)
=> Ob là tia phân giác
Do Oa là tia phân giác của góc xOy
=> góc xOa= góc aOy = góc xOa . \(\frac{1}{2}\) =70. \(\frac{1}{2}\) =35o
có góc xOy và góc x'Oy là hai góc kề bù
=> góc xOy + góc x'Oy=180 o
Thay số: 70o+ góc x'Oy=180o
góc x'Oy=180o-70o
góc x'Oy=1100
có góc x'Oy và x'Oy' là hai góc kề bù
=> góc x'Oy + x'Oy'=180o
Thay số: 110o+ góc x'Oy'=180o
góc x'Oy'=180o-110o
góc x'Oy'=70o
Có tia Ox nằm giữa 2 tia Oa và Oy'
=>góc aOx+ góc xOy'=góc aOy'
Thay số: 35o+110o=góc aOy'
góc aOy'=110o+35o
góc aOy'=145o
có góc bOy' và góc aOy' là 2 góc kề nhau
=> góc bOy'+ góc aOy'=180o
Thay số: góc bOy'+145o=180o
góc bOy'=180o-145o
góc bOy'=35o
có Ob nằm giữa 2 tia Ox' và Oy'
=> góc x'Ob+ góc bOy'=x'Oy'
Thay số: góc x'Ob +35o=70o
góc x'Ob=70o-35o
góc x'Ob=35o
góc x'Ob=góc bOy'=35o (1)
Tia Ob nằm giữa hai tia Ox' và Oy' (2)
Từ (1) và (2)
Vậy tia Ob là phân giác cảu góc x'Oy'

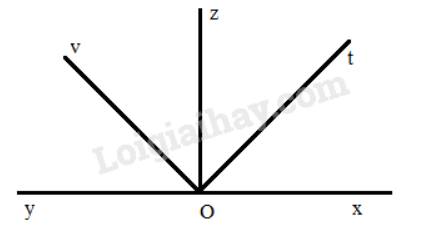
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\) = \(\frac{1}{2}.180^\circ = 90^\circ \)
Vì Ot là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {xOt} = \widehat {tOz} = \frac{1}{2}\widehat {xOz} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì Ov là tia phân giác của \(\widehat {zOy}\) nên \(\widehat {yOv} = \widehat {vOz} = \frac{1}{2}\widehat {zOy} = \frac{1}{2}.90^\circ = 45^\circ \)
Mà tia Oz nằm trong \(\widehat {tOv}\) nên \(\widehat {tOv}= \widehat {tOz} + \widehat {zOv} = 45^\circ + 45^\circ = 90^\circ \)
Vậy \(\widehat {tOv} = 90^\circ \)

\(\widehat{aOy}=\dfrac{\widehat{xOy}}{2}\)
\(\widehat{bOy}=\dfrac{\widehat{zOy}}{2}\)
Do đó: \(\widehat{aOy}+\widehat{bOy}=\dfrac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\dfrac{1}{2}\cdot180^0\)
hay \(\widehat{aOb}=90^0\)(đpcm)
a)
Vì Oa là phân giác của xOy => yOa = xOa = 90 : 2 = 45độ
Vì Ob là phân giác của xOa => xOb = aOb = 45 : 2 = 22,5độ
Vì Oc là phân giác của xOb => xOc = bOc = 22,5 : 2 = 11,25
b)
Mk đang nghĩ :V
b)
Để xOc nhỏ nhất thì xOb nhỏ nhất
Để xOb nhỏ nhất thì xOa nhỏ nhất
Để xOa nhỏ nhất thì xOy nhỏ nhất
=> ko tìm đc giá trị chính thức nhưng :
để xOc nhỏ nhất thì xOy phải nhỏ nhất
P/s : ko chắc