Cho a và b là các số tự nhiên. CMR nếu a mũ 3 + b mũ 3 chia hết cho 3 thì a+b chia hết cho 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(a^3-a=a\left(a-1\right)\left(a+1\right)\)
Vì a;a-1;a+1 là ba số nguyên liên tiếp
nên \(a\left(a-1\right)\left(a+1\right)⋮3!\)
hay \(a^3-a⋮6\)

Bài này cần dùng một ít kiến thức của lớp 8, bạn có thể tìm hiểu thêm.
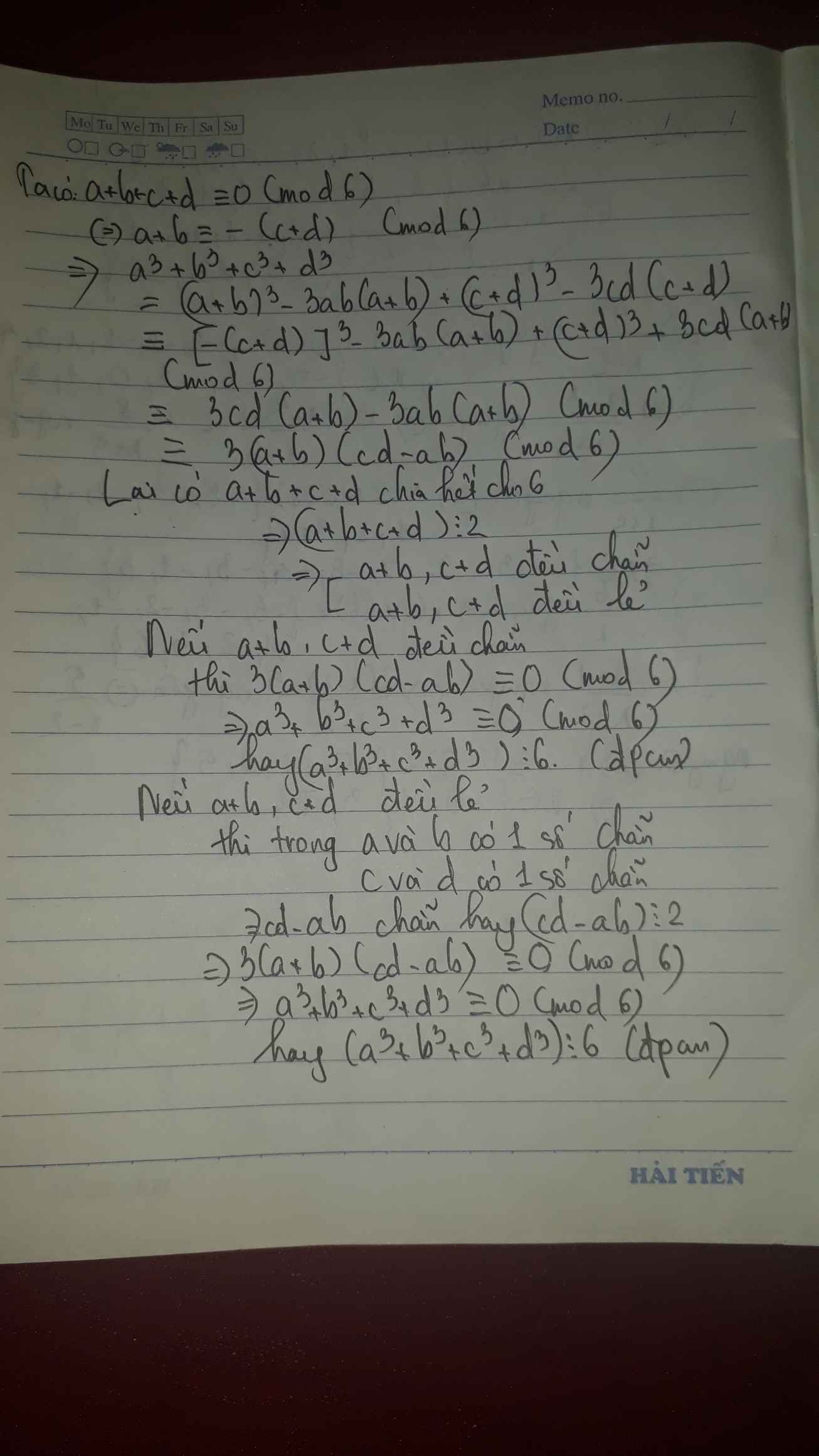

a) Phần này dễ, bạn cứ làm theo hướng của phần b là được. Mình sẽ làm phần b khó hơn.
b) Ta có: a3-a = a.(a-1).(a+1) (với a thuộc Z). Mà a.(a-1).(a+1) là tích của 3 số tự nhiên liên tiếp nên
a.(a-1).(a+1) chia hết cho 3.
=> a3- a chia hết cho 3.
Chứng minh tương tự ta có b3 - b chia hết cho 3 và c3 - c chia hết cho 3 với mọi b,c thuộc N.
=> a3+b3+c3 - (a+b+c) luôn chia hết cho 3 với mọi a,b,c thuộc N.
Do đó nếu a3+b3+c3 chia hết cho 3 thì a+b+c chia hết cho 3 và điều ngược lại cũng đúng.
Vậy đpcm.
Tớ làm thêm một cách cho câu b nhé ;)
Ta có: \(a^3+b^3⋮3\Rightarrow a^3+b^3+3a^2b+3ab^2-3a^2b-3ab^2⋮3\) \(\Rightarrow\left(a+b\right)^3-3ab\left(a+b\right)⋮3\)
Do a và b là các số tự nhiên => \(3ab\left(a+b\right)⋮3=>\left(a+b\right)^3⋮3\)
=> a+b chia hết cho 3

Bg
a) Gọi số chẵn nhỏ nhất trong ba số chẵn liên tiếp là 2x (x \(\inℤ\))
=> Tổng ba số chẵn liên tiếp = 2x + (2x + 2) + (2x + 4)
=> 2x + (2x + 2) + (2x + 4) = 2x + 2x + 2 + 2x + 4
=> 2x + (2x + 2) + (2x + 4) = (2x + 2x + 2x) + (2 + 4)
=> 2x + (2x + 2) + (2x + 4) = 2.3x + 6
=> 2x + (2x + 2) + (2x + 4) = 6x + 6.1
=> 2x + (2x + 2) + (2x + 4) = 6.(x + 1) \(⋮\)6
=> Tổng ba số tự nhiên liên tiếp chia hết cho 6
=> ĐPCM
b) Bg
Tổng ba số lẻ liên tiếp luôn là một số lẻ
Mà 6 chẵn
=> Tổng của ba số lẻ liên tiếp không chia hết cho 6
=> ĐPCM
c) Bg
Ta có: a \(⋮\)b và b \(⋮\)c (a, b, c \(\inℤ\))
Vì a \(⋮\)b
=> a = by (bởi y \(\inℤ\))
Mà b \(⋮\)c
=> by \(⋮\)c
=> a \(⋮\)c
=> ĐPCM
d) Bg
Ta có: P = a + a2 + a3 +...+ a2n (a, n\(\inℕ\))
=> P = (a + a2) + (a3 + a4)...+ (a2n - 1 + a2n)
=> P = [a.(a + 1)] + [a3.(a + 1)] +...+ [a2n - 1.(a + 1)]
=> P = (a + 1).(a + a3 + a2n - 1) \(⋮\)a + 1
=> P = a + a2 + a3 +...+ a2n \(⋮\)a + 1
=> ĐPCM (Điều phải chứng mình)
\(a^3+b^3\) chia hết 3
\(a^3+b^3-a-b=a\left(a-1\right)\left(a+1\right)+b\left(b+1\right)\left(b-1\right)\) chia hết 3
nên a+b chia hết 3 =))
Lời giải:
Ta có:
\(a^3+b^3\vdots 3\)
\(\Leftrightarrow a^3+b^3+3a^2b+3ab^2\vdots 3\)
\(\Leftrightarrow (a+b)^3\vdots 3\)
Mà do $3$ là số nguyên tố nên \(\Rightarrow a+b\vdots 3\) (đpcm)