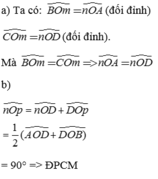2 đường thẳng ab và cd cắt nhau tại o om là tia phân giác của aoc chứng minh tia đối của om là phân giác của bod
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có : 2 đường thẳng AB và CD cách nhau tại O sẽ tạo ra các góc đối đỉnh
=>AOC=BOD [2 góc đối dỉnh]
TA CÓ: OM và ON lần lượt là tia phân giác của AOC ,BOD
Suy ra OM và ON là 2 tia đối nhau

Câu hỏi của Phương Thảo - Toán lớp 7 - Học toán với OnlineMath
Bạn tham khảo
#) Tham khảo
góc AOC + COB = 180đ (kề bù)
có AOC = DOB và vì OM, ON là tia phân giác 2 góc này nên MOC = NOB
=> MOC + NOB = AOC (*)
CÓ MOC + COB + NOB mà từ (*) => MOC + COB + NOB= AOC +COB và bằng 180 độ
2 tia OM và ON có chung đỉnh O và tạo vs nhau một góc = 180 độ
=> OM và ON là 2 tia đối nhau
~ Hok tốt ~

ON là phân giác góc DOB
Chứng minh:
Ta có: ^DOn = ^COm ( đối đỉnh)
^BOn = ^AOm ( đối đỉnh)
Mà ^AOm = ^COm ( Om là phân giác góc AOC)
-> ^DOn = ^BOn
=> On là phân giác góc DOB
Bài giải
Ta có : Hai đường thẳng AB và CD cắt nhau tại O
\(\Rightarrow\) Sẽ tạo thành hai cặp góc đổi đỉnh
Mà hai góc đối đỉnh thì bằng nhau \(\Rightarrow\) \(\widehat{AOC}=\widehat{BOD}\) , \(\widehat{AOD}=\widehat{COB}\)
Mà On là tia đối của Om ( Om là tia phân giác của góc AOC )
\(\Rightarrow\) On là tia phân giác của góc \(BOD\)