Tam giác ABC có AB=16, AC=18, góc B=60 độ. Tính BC
(ko có đơn vị độ dài)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 6 2015
Kẻ trung tuyến AM
TAm giác ABC có AM là trung tuyến
=> AM = MC=1/2 BC
TAm giác AMC có AM =MC và C = 60 độ => tam giác AMC đều
=> AC = AM = 1
ta lại có AM = 1/2 BC => BC= 2AM = 2.1 = 2
TAm giác ABC vuông tại A , theo py ta go
AB^2 + AC^2 = BC ^2
=> AB ^2 = BC^2 - AC^2
= > AB^2 = 2^2 - 1^2
= 4 - 1 = 3
=>AB = căn 3
DL
2
10 tháng 8 2019
Cách 3: (Lớp 8) Trên nửa mặt phẳng bờ AC không chứa B, dựng tam giác đều ACG.
Có ngay AB = AC = AG và ^BAG = ^BAC + ^CAG = 900 => \(\Delta\)BAG vuông cân tại A
Suy ra ^CBG = ^ABC - ^ABG = 300 = ^DAB (1)
Cũng dễ thấy ^ADB = 1350; ^BCG = ^ACB + ^ACG = 1350 => ^BCG = ^ADB (2)
Từ (1) và (2) suy ra \(\Delta\)CGB ~ \(\Delta\)DBA (g.g). Từ đây \(\frac{AD}{BC}=\frac{AB}{BG}=\frac{1}{\sqrt{2}}\)
Vậy \(AD=\frac{BC}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)(cm).
9 tháng 8 2019
Trên nửa mặt phẳng bờ BC chứa A dựng \(\Delta\)BCE vuông cân tại E
Khi đó ^EBA = ^ABC - ^EBC = 300 = ^DAB
\(\Delta\)AEC = \(\Delta\)AEB (c.c.c) => ^EAB = ^BAC/2 = 150 = ^DBA
Xét \(\Delta\)BEA và \(\Delta\)ADB có: AB chung, ^EAB = ^DBA, ^EBA = ^DAB
=> \(\Delta\)BEA = \(\Delta\)ADB (g.c.g) => AD = BE = \(\frac{BC}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)(cm).
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 7 2021
Kẻ đường cao BH (H thuộc AC)
Do góc A nhọn \(\Rightarrow\) H nằm giữa A và C
Ta có: \(S_{ABC}=\dfrac{1}{2}BH.AC\Leftrightarrow\dfrac{2}{5}bc=\dfrac{1}{2}BH.b\)
\(\Rightarrow BH=\dfrac{4c}{5}\)
Áp dụng Pitago cho tam giác vuông ABH:
\(AH^2=AB^2-BH^2=c^2-\left(\dfrac{4c}{5}\right)^2=\dfrac{9c^2}{25}\Rightarrow AH=\dfrac{3c}{5}\)
\(\Rightarrow CH=AC-AH=b-\dfrac{3c}{5}\)
Pitago tam giác vuông BCH:
\(BC=\sqrt{BH^2+CH^2}=\sqrt{\left(\dfrac{4c}{5}\right)^2+\left(b-\dfrac{3c}{5}\right)^2}=\sqrt{b^2-\dfrac{6}{5}bc+c^2}\)
VS
11 tháng 7 2018
75% = 3/4
Tổng độ dài AB và AC là: 3 + 4 = 7 (phần)
Giá trị 1 phần: 120 : ( 3 + 4 + 5) = 10 (cm)
Cạnh AC: 10 x 3 = 30 (cm)
Cạnh AB: 10 x 4 = 40 (cm)
Cạnh BC: 10 x 5 = 50 ( cm)
DT tam giác ABC:( 30 x 40): 2= 60 (cm2)
Chiều cao tương ứng của cạnh BC: 60 x 2 : 50 = 24
Học Tốt ^-^
BB
1
14 tháng 8 2018
-Áp dụng định lí: Trong một tam giác vuông, đoạn thẳng đối diện với góc 30o thì bằng \(\frac{1}{2}\)cạnh huyền
=> \(AB=\frac{1}{2}.BC\)=> BC = 2. AB = 2. 3 = 6 (cm)
-Tam giác ABC vuông tại A, theo định lí Pytago, ta có:
BC2 = AB2 + AC2
=> 62 = 32 + AC2
=> AC2 = 36 - 9 = 27
=> \(AC=\sqrt{27}\) (cm)
MC
21 tháng 1 2016
Ta có: AC^2 = AB^2 +BC^2 - 2AB.BC.cos(ABC)
<=> 14^2 = 16^2 +BC^2 -2.16.BC.cos(60)
<=> BC^2 - 16BC + 60 = 0
<=> BC = 6 hoặc BC=10
Với BC=6 hoặc BC=10 đều thỏa mãn tổng 2 cạnh lớn hơn 1 cạnh
Vậy BC=6 hoặc BC=10
trong một tg nhọn thì bình phương một cạnh bất kì bằng tổng bình phương cạnh thứ 2 và bình phương cạnh thứ 3 trừ cho 2. cạnh 2 .cạnh 3 . cos góc tạo bởi cạnh 2 và cạnh 3
cho tg nhọn ABC có cạnh AB=c AC=b BC=a kẻ đường cao BH
ta có HC^2= (AC-AH)^2 <=> BH^2 + HC^2 = AC^2 + AB^2 - 2AB.AC.AH/AB
<=> a^2=b^2+c^2-2bc.cosBAC => đpcm
như nnafy hả
NX
23 tháng 8 2023
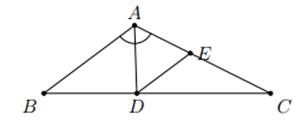
\(\text{Đặt AD=DE=EA=x. Ta có}\)
\(\text{Đặt AD=DE=EA=x. Ta có:}\)
\(\dfrac{DE}{AB}=\dfrac{CE}{CA}=\dfrac{x}{3}=\dfrac{6-x}{6}\)
\(\Rightarrow x=2\). \(\text{Vậy}\) \(AD=2cm\)