cho tam giác ABC có D là trung điểm của AB.Điểm E thuộc cạnh AC sao cho DE//BC.Chứng minh rằng E là trung điểm của AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: AD=AE
=> Tam giác ADE cân tại A
\(\Rightarrow\widehat{ADE}=\dfrac{180^0-\widehat{A}}{2}\)
Mà \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Tam giác ABC cân tại A)
=> \(\widehat{ADE}=\widehat{ABC}\)
Mà 2 góc này đồng vị
=> DE//BC
b) Xét tam giác ABI và tam giác ACI
AB=AC
AI chung
BI=IC
=> ΔABI=ΔACI
=> \(\widehat{AIB}=\widehat{AIC}=180^0:2=90^0\Rightarrow AI\perp BC\)
=> AI là đường trung trực của BC

Vì DF // AE (DF//AB; E ) nên (2 góc so le trong)
Hay ( I )
Xét và có:
(c/m trên)
IE=IF(I là trung điểm của EF)
(2 góc đối đỉnh)
=>
=> IA=IB( 2 cạnh tương ứng). Mà I nằm giữa A và B
=> I là trung điểm của AB
Vì DF // AE (DF//AB; E ∈AB∈AB) nên ˆAEF=ˆEFDAEF^=EFD^ (2 góc so le trong)
Hay ˆAEI=ˆIFDAEI^=IFD^ ( I ∈EF∈EF )
Xét ΔAEIΔAEI và ΔDFIΔDFI có:
ˆAEI=ˆIFDAEI^=IFD^ (c/m trên)
IE=IF(I là trung điểm của EF)
ˆAIE=ˆDIFAIE^=DIF^ (2 góc đối đỉnh)
=> ΔAEI=ΔDFI(g.c.g)ΔAEI=ΔDFI(g.c.g)
=> IA=IB( 2 cạnh tương ứng). Mà I nằm giữa A và B
=> I là trung điểm của AB

vì DE // BC
=> DN // BM
VÀ EN // MC
=> DN/BM = EN/CM = AN/AM
=> DN = CN

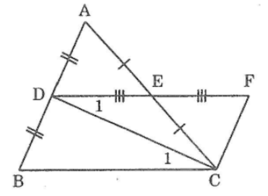
Ta có: ΔBDC= ΔFCD(chứng minh trên)
Suy ra: ∠(C1 ) =∠(D1 ) (hai góc tương ứng)
Suy ra: DE // BC ( vì có hai góc so le trong bằng nhau)
ΔBDC= ΔFCD suy ra BC = DF (hai cạnh tương ứng)
Mà DE = 1/2 DF(gt). Vậy DE = 1/2 BC