Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
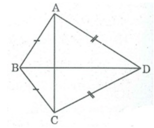
Ta có:
* BA = BC (gt)
Suy ra B thuộc đường trung trực của AC
* DC = DA (gt)
Suy ra D thuộc đường trung trực của AC
Mà B ≠ D nên BD là đường trung trực của AC
Do đó A đối xứng với C qua trục BD.
Có hình vẽ :
Lấy trung điểm M của BC . Kẻ MM,MM, vuông góc B'C' => MM' = 1212(BB'+CC')(1)
△GMM′∼△GAA′(g.g)=>MM′AA′=GMAG=12△GMM′∼△GAA′(g.g)=>MM′AA′=GMAG=12(2)
Từ (1);(2) => AA'=BB'+CC'
1b Lấy trung điểm M của BC . Kẻ MM' vuông góc với B'C' . Lấy E là trung điểm AG => AE=EG=GM
=>EE′=12(AA′+GG′);GG′=12(MM′+EE′)=>MM′+AA′+GG′2=2GG′=>2MM′+AA′=3GG′=>AA′+BB′+CC′=3GG′
P/s: Tham khảo nha
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
ta có: BC=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra BD là đường trung trực của AC
hay A và C đối xứng nhau qua BD
1: Xét tứ giác ADCE có
AE//CD
AE=CD
Do đó: ADCE là hình bình hành
mà DA=DC
nên ADCE là hình thoi
1: Xét tứ giác ADCE có
AE//CD
AE=CD
Do đó: ADCE là hình bình hành
mà DA=DC
nên ADCE là hình thoi
a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của DC
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành
