mn giúp em với ạ, em cảm ơn ^^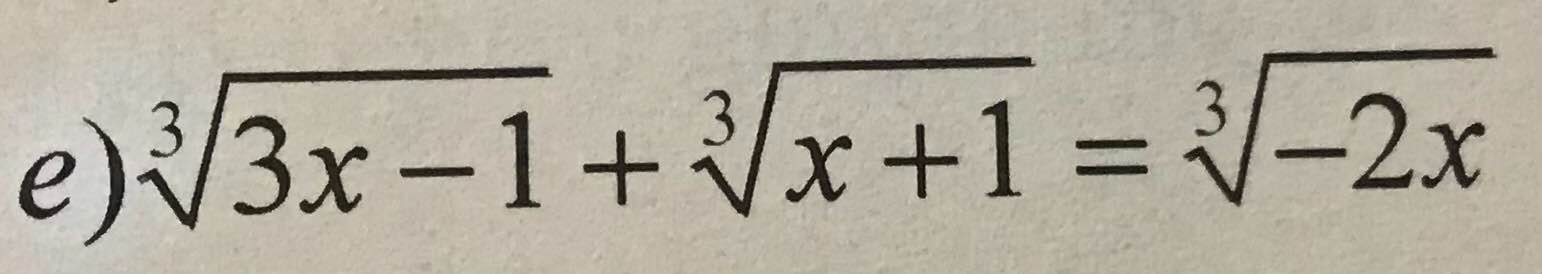
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
mn giúp em và giair thích giúp em với ạ em cảm ơn mn
1
28 tháng 1 2023
2. get lucky money
3. talent show
4. always
5. food stands
6. fireworks
7. never
8. eat traditional foods
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(h'\left(x\right)=f'\left(x\right)-g'\left(x\right)=0\Rightarrow x=\left\{a;b;c\right\}\)
Ta thấy \(h'\left(x\right)>0\) trên \(\left(b;c\right)\) và \(h'\left(x\right)< 0\) trên \(\left(a;b\right)\)
\(\Rightarrow x=b\) là điểm cực tiểu trên \(\left[a;c\right]\) hay \(\min\limits_{\left[a;c\right]}h\left(x\right)=h\left(b\right)\)
NQ
0
TT
0
LC
1
3 tháng 8 2021
\(=>Qthu1=0,2.340000=68000J\)
\(=>Qthu2=2100.0,2.20=8400J\)
\(=>Qtoa=2.4200.25=210000J\)
\(=>Qthu1+Qthu2< Qtoa\)=>đá nóng chảy hoàn toàn
\(=>0,2.2100.20+0,2.340000+0,2.4200.tcb=2.4200\left(25-tcb\right)\)
\(=>tcb=14,5^oC\)
3 tháng 8 2021
Cho em hỏi ngu tí ạ vậy tcb ở nhưng phép tính trên vứt đi đâu ạ
Đặt \(\left\{{}\begin{matrix}\sqrt[3]{3x-1}=a\\\sqrt[3]{x+1}=b\\\sqrt[3]{-2x}=c\end{matrix}\right.\) ta được hệ:
\(\left\{{}\begin{matrix}a+b=c\\a^3+b^3=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\\left(a+b\right)^3-3ab\left(a+b\right)=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c^3-3abc=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left(c^2-ab\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left[\left(a+b\right)^2-ab\right]=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left[\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\right]=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}c=0\\a=b=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt[3]{-2x}=0\Leftrightarrow x=0\)