cho tam giác DEF ( DE<DF ) tia Dx đi qua trung điểm k của EF kẻ EH, FM cùng vuông góc với so sánh EH và FM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 1 2022
ta thấy 3x3+4x4=5x5 nên nó là tam giác vuông
diện tích là S=1/2x3x4=6(cm2)
chúc bạn học tốt
HYC-23/1/2022
NT
1
28 tháng 11 2021
\(\widehat{D}=180^0-\widehat{E}-\widehat{F}=50^0=\widehat{A}\\ \left\{{}\begin{matrix}AB=DE\\\widehat{A}=\widehat{D}\\AC=DE\end{matrix}\right.\Rightarrow\Delta ABC=\Delta DEF\left(c.g.c\right)\)
17 tháng 8 2017
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
I
22 tháng 2 2020
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
25 tháng 2 2022
Xét
DE^2 + DF^2 = 3^2 + 4^2 = 9 + 16 = 25
EF^2 = 5^2 = 5
=> DE^2 + DF^2 = EF^2
=> DEF là tam giác vuông
3 tháng 7 2021
\(\Delta DEF\) cho ta \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{D}=180^0-\left(\widehat{E}+\widehat{F}\right)\)
\(\Rightarrow\widehat{D}=180^0-\left(70^0+60^0\right)=180^0-130^0=50^0\)
\(Xét\) \(\Delta ABCvà\Delta DEFcó\)
\(\widehat{A}=\widehat{D}\left(=50^0\right)\)
AB=DE
AC=DF
\(\Rightarrow\Delta ABC=\Delta DEF\left(c-g-c\right)\)
Vậy \(\Delta ABC=\Delta DEF\)
I
22 tháng 2 2020
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
11 tháng 4 2020
Cho tam giác ABC và tam giác DEF có: AB=DE,BC=EF,AC=DF.
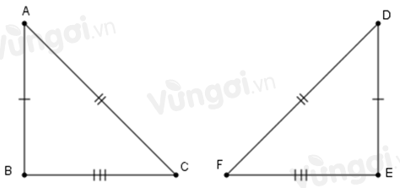
Xét ΔABC và ΔDEF có:
AB=DE(gt)
BC=EF(gt)
AC=DF(gt)
⇒ΔABC=ΔDEF (c.c.c).
Học tốt nhé!
TT
1