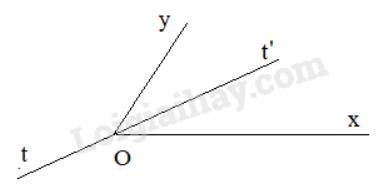
Cho \(\widehat{xOy}=120^o\) , Ot là tia phân giác của \(\widehat{xOy}\) . Trên Oy lấy điểm A. Qua A vẽ tia At' // Ot và tia Ax' // Ox.
a, Tính \(\widehat{xOt}\) và \(\widehat{tOy}\)
b, Tính \(\widehat{yAt'}\) và \(\widehat{yAx'}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
2 tháng 4 2021
Vì xOt = 30 , xOy = 60
=> xOt < xOy Mà Ot, Oy cùng nằm trên nửa mặt phẳng bờ Ox
=> Ot nằm giữa Ox và Oy.
Vì Ot nằm giữa Ox và Oy
=> tOx + tOy = xOy
=> 30 + tOy=60
=> tOy=30 Mà tOx=30
=> tOy= tOx
Vì tOy = tOx ; Ot nằm giữa Ox và Oy
=> Ot là tia phân giác góc xOy
2 tháng 4 2021
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOt}< \widehat{xOy}\left(30^0< 60^0\right)\)
nên tia Ot nằm giữa hai tia Ox và Oy
LH
8 tháng 8 2018
a) Ta có : Ot là tia phân giác của góc xOy
=> ∠xOt = ∠tOy = 60
b)+ Ta có : Ax' // Ox
=> ∠xOy = ∠x'Ay = 120
+ Ta có : At' // Ot
=> ∠tOy = ∠t'Ay = 60
Hình bn tự vẽ nha,mình ko ghi độ dc nhé
T
21 tháng 7 2018
a/Vì \(\widehat{xOy}>\widehat{xOt}\)\(\left(70^o>35^o\right)\)nên Ot nằm giữa Õ và Oy
Ta có : \(\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\)
Thay : \(35^o+\widehat{tOy}=70^o\)
\(\Rightarrow\widehat{tOy}=70^o-35^o\)
\(\Rightarrow\widehat{tOy}=35^o\)
b/ Ot hay Oy [ mình nghĩ bạn ghi sai đề, đáng lẽ là Ot chứ ]
Ot là tia phân giác của \(\widehat{xOy}\)vì Ot nằm giữa và \(\widehat{xOt}=\widehat{tOy}=35^o\)
c/
Vì Om là tia đối của Ot nên \(\widehat{tOy}\)và \(\widehat{mOy}\)kề bù :
Nên : \(\widehat{tOy}+\widehat{mOy}=180^o\)
Thay : \(35^o+\widehat{mOy}=180^o\)
\(\Rightarrow\widehat{mOy}=180^o-35^o\)
Vậy : \(\widehat{mOy}=145^o\)
18 tháng 4 2017
Giải:
a) Tia Ot nằm giữa hai tia Ox và Oy (1) vì các tia Ot,Oy cùng thuộc nửa
mặt phẳng bờ chứa Ox và <
b) Tia Ot nằm giữa hai tia Ox,Oy nên:
+
=
do đó
250+ = 500
suy ra = 500- 250 =250 vậy
=
(2)
c) từ (1) và (2) suy ra Ot là tia phân giác của góc xOy.
PG
21 tháng 4 2017
a) Vì trên cùng một nửa mặt phẳng bờ chứa tia Ox có \(\widehat{xOt}< \widehat{xOy}\left(25^0< 50^o\right)\)
Nên tia Ot nằm giữa 2 tia Oy và Ot (1)
\(\Rightarrow\) \(\widehat{xOt}+\widehat{yOt}=\widehat{xOy}\)
Thay \(\widehat{xOt}=25^{o^{ }};\widehat{xOy}=50^{o^{ }}\)
b) Ta có:
\(25^{o^{ }}+\widehat{yOt}=50^{o^{ }}\)
\(\Rightarrow\)\(\widehat{yOt}=\)\(50^o-25^o=25^{o^{ }}\)
Có \(\left\{{}\begin{matrix}\widehat{tOy}=25^{o^{ }}\\\widehat{xOt}=25^o\end{matrix}\right.\Rightarrow\widehat{tOy}=\widehat{xOt}\)(2)
c) Từ (1) và (2)
\(\Rightarrow\) Tia Ot là tia phân giác của \(\widehat{xOy}\)
9 tháng 4 2021
a) Ta có: \(\widehat{xOm}+\widehat{yOm}=180^0\)(Hai góc kề bù)
\(\Leftrightarrow\widehat{yOm}+30^0=180^0\)
hay \(\widehat{yOm}=150^0\)
Vậy: \(\widehat{yOm}=150^0\)
9 tháng 4 2021
b) Ta có: tia Ot là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{yOt}=\widehat{xOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{180^0}{2}\)
hay \(\widehat{yOt}=90^0\)(đpcm)
18 tháng 9 2023
(1) đúng vì Ot là tia phân giác của góc xOy thì \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy}\)
(2) sai vì
Gọi Ot’ là tia phân giác của góc xOy, ta có: \(\widehat {xOt'} = \widehat {t'Oy}\)
Xét tia Ot là tia đối của tia Ot' thì \(\widehat {xOt'}+ \widehat {xOt}= 180^0; \widehat {t'Oy}+\widehat {tOy}=180^0\) (kề bù)
Ta có: \(\widehat {xOt} = \widehat {tOy}\) nhưng Ot không là tia phân giác của góc xOy.
Chú ý:
Mỗi góc khác góc bẹt chỉ có một tia phân giác.
KM
30 tháng 3 2019
Bạn tự vẽ hình nhé!
a. Vì \(\widehat{xOt}>\widehat{xOy}\)
=> Ot nằm giữa 2 tia Ox và Oy
Ta có:\(\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\)
Thay:\(\widehat{xOt}=120^o,\)\(\widehat{xOy}=180^0\)
=>\(\widehat{yOt}=180^0-120^0\)
Vậy:\(\widehat{yOt}=60^0\)
b. \(\widehat{yOz}=\widehat{xOy}:2\)
Thay:\(\widehat{xOy}=180^0\)
=>\(\widehat{yOx}=180^0:2\)
Vậy:\(\widehat{yOx}=90^0\)
\(\widehat{zOt}=\widehat{xOt}-\widehat{xOz}\)
Thay:\(\widehat{xOt}=120^0,\widehat{xOz}=90^0\)
=>\(\widehat{zOt}=120^0-90^0\)
Vậy:\(\widehat{xOt}=30^0\)
c. Mình thấy đề hơi sai sai thì phải, góc xOy= 180^0 mà Om là tia đối của Ox thì chẳng lẽ Om là Oy hả?
Hình bạn tự vẽ nha
a, Vì Ot là phân giác \(\widehat{xOy}\)=> \(\widehat{xOt}\)\(=\widehat{tOy}\)\(=\frac{1}{2}120^o\)\(=60^o\)
b, Vì At'//Ot => \(\widehat{yAt'}=\widehat{AOt}\)\(=60^o\) ( 2 góc đồng vị)
Vì Ax'// Ox=>\(\widehat{yAx'}=\widehat{AOx}=70^o\)
chúc bạn học tốt
bổ sung câu b, cho mình : vì nó là 2 góc đồng vị nên bằng nhau chỗ \(\widehat{yAx'}\)nha