giải phương trình:\(x^2-x-18+\dfrac{72}{x^2-x}=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
L
1
17 tháng 10 2021
Đk: \(x\ne5;x\ne-10\)
Pt: \(\Rightarrow\dfrac{\left(x-2\right)\left(x+5\right)}{x^2}-\dfrac{40}{\left(x-5\right)\left(x+10\right)}=0\)
\(\Rightarrow\left(x-2\right)\left(x+5\right)\left(x-5\right)\left(x+10\right)-40x^2=0\)
\(\Rightarrow\left(x^2-12x+20\right)\left(x^2-25\right)-40x^2=0\)
\(\Rightarrow x^4-12x^3-45x^2+300x=500\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\left(loại\right)\\x=-5\left(tm\right)\end{matrix}\right.\)
6 tháng 10 2021
\(\sqrt{\dfrac{72x}{128}}=\dfrac{3}{4}\)
\(\Leftrightarrow x\cdot\dfrac{9}{16}=\dfrac{9}{16}\)
hay x=1
PN
18 tháng 5 2021
\(2x^2+3x-5=0\)
\(< =>2x^2-2x+5x-5=0\)
\(< =>2x\left(x-1\right)+5\left(x-1\right)=0\)
\(< =>\left(x-1\right)\left(2x+5\right)=0\)
\(< =>\orbr{\begin{cases}x=1\\x=-\frac{5}{2}\end{cases}}\)
PN
18 tháng 5 2021
\(\hept{\begin{cases}x+2y=1\\-3x+4y=-18\end{cases}}\)
\(< =>\hept{\begin{cases}-3x-6y=-3\\-3x-6y+10y=-18\end{cases}}\)
\(< =>\hept{\begin{cases}x+2y=1\\10y=-18+3=-15\end{cases}}\)
\(< =>\hept{\begin{cases}x+2y=1\\y=-\frac{3}{2}\end{cases}< =>\hept{\begin{cases}x-3=1\\y=-\frac{3}{2}\end{cases}< =>\hept{\begin{cases}x=4\\y=-\frac{3}{2}\end{cases}}}}\)
HH
10 tháng 4 2021
a) x^2 - 3x + 2 = 0
\(\Delta=b^2-4ac=\left(-3\right)^2-4.1.2=1\)
=> pt có 2 nghiệm pb
\(x_1=\frac{-\left(-3\right)+1}{2}=2\)
\(x_2=\frac{-\left(-3\right)-1}{2}=1\)
10 tháng 4 2021
a) Dễ thấy phương trình có a + b + c = 0
nên pt đã cho có hai nghiệm phân biệt x1 = 1 ; x2 = c/a = 2
b) \(\hept{\begin{cases}x+3y=3\left(I\right)\\4x-3y=-18\left(II\right)\end{cases}}\)
Lấy (I) + (II) theo vế => 5x = -15 <=> x = -3
Thay x = -3 vào (I) => -3 + 3y = 3 => y = 2
Vậy pt có nghiệm ( x ; y ) = ( -3 ; 2 )
PN
1
LN
1
11 tháng 5 2020
\(x^2-x=x\left(x-1\right)\)
ĐKXĐ: \(x\ne0;x\ne1\)
\(x^2-x-18+\frac{72}{x^2-x}=0\)
\(\Leftrightarrow\left(x^2-x-18\right)\left(x^2-x\right)+72=0\Leftrightarrow\left(x^2-x\right)^2-18\left(x^2-x\right)+72=0\)
\(\Leftrightarrow\left(x^2-x-9\right)^2-3^2=0\)
\(\Leftrightarrow\left(x^2-x-6\right)\left(x^2-x-12\right)=0\)
\(\Leftrightarrow x=\left\{3;-2;-3;4\right\}\)
XD
1
22 tháng 3 2022
\(\Leftrightarrow\dfrac{4x-3x}{72}=\dfrac{3}{2}\\ \Leftrightarrow\dfrac{x}{72}=\dfrac{3}{2}\\ \Leftrightarrow x=108\)
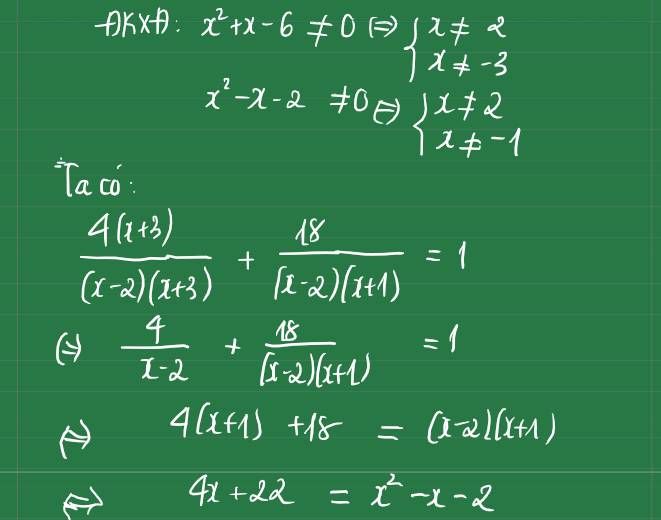
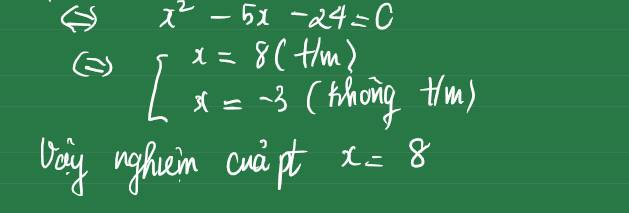
\(x^2-x-18+\dfrac{72}{x^2-x}=0\) ( ĐK : \(x\ne0\) và \(x\ne1\) )
\(\Leftrightarrow x^2-x+\dfrac{72}{x^2-x}=18\)
Đặt \(x^2-x=a\) . Phương trình trở thành :
\(a+\dfrac{72}{a}=18\)
\(\Leftrightarrow a^2-18a+72=0\)
\(\Leftrightarrow\left(a-6\right)\left(a-12\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-6=0\\a-12=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=6\\a=12\end{matrix}\right.\)
Với \(a=6\) :
\(\Leftrightarrow x^2-x=6\)
\(\Leftrightarrow x^2-x-6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)
Với \(a=12\) :
\(\Leftrightarrow x^2-x=12\)
\(\Leftrightarrow x^2-x-12=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
Vậy \(S=\left\{-2;-3;3;4\right\}\)