cho hình vẽ chung minh rang Ax//By//Cz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CA
6 tháng 10
*Kẻ By’ là tia đối của tia By => ABy kề bù với ABy’
=> ABy + ABy’ = 180
=> 120 + ABy’ = 180
=> ABy’ = 60
Ta có mAx = 60 =ABy’ , mà mAx và ABy’ ở vị trí đồng vị => Ax // By (1)
*Ta có yBC + CBA + ABy = 360
=> yBC + 90 + 120 = 360
=> yBC = 150
Ta có BCz = 150 = yBC, mà 2 góc này ở vị trí so le trong => By // Cz (2)
Từ (1), (2) => đpcm
PT
1
CM
15 tháng 6 2018
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
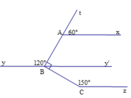
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
VD
2
KR
2
8 tháng 7 2016
Áp dụng bất đẳng thức Bunhiacopxki, ta được : \(\left(a+b+c\right)\left(x+y+z\right)\ge\left(ax+by+cz\right)^2=\left(3ax\right)^2=30^2=90\)
\(\Rightarrow\left(a+b+c\right)\left(x+y+z\right)\ge90\)
8 tháng 7 2016
Xin lỗi bạn nhé ^^
Tại vội quá nên mình nhìn lộn. Phải là 900 mới đúng.
Nhưng như vậy thì có thể đề bài chưa đúng.
25 tháng 11 2018
Ta có \(ax^3=by^3=cz^3\Leftrightarrow\dfrac{ax^2}{\dfrac{1}{x}}=\dfrac{by^2}{\dfrac{1}{y}}=\dfrac{cz^2}{\dfrac{1}{z}}=\dfrac{ax^2+by^2+cz^2}{\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}}=ax^2+by^2+cz^2\Leftrightarrow\sqrt[3]{ax^2+by^2+cz^2}=\sqrt[3]{ax^3}=\sqrt[3]{by^3}=\sqrt[3]{cz^3}=\dfrac{\sqrt[3]{a}}{\dfrac{1}{x}}+\dfrac{\sqrt[3]{b}}{\dfrac{1}{y}}+\dfrac{\sqrt[3]{c}}{\dfrac{1}{z}}=\dfrac{\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}}{\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}}=\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\)Vậy \(\sqrt[3]{ax^2+by^2+cz^2}=\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\)
Mik ko thấy hình