abc+acd=bca
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
27 tháng 1 2022
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)
DT
15 tháng 4 2019
hình dễ nên tự vẽ
a, xét 2 t.giác vuông ABM và HBM có:
BM cạnh chung
\(\widehat{ABM}\)=\(\widehat{HBM}\)(gt)
=> t.giác ABM=t.giác HBM(cạnh huyền- góc nhọn)
=> AB=BH(2 cạnh tương ứng)
b, ta có: \(\widehat{ABM}\)+\(\widehat{BAM}\)+\(\widehat{AMB}\)=180 độ
=>30 độ+90 độ +\(\widehat{AMB}\)=180 độ
=>\(\widehat{AMB}\)=60 độ mà \(\widehat{AMB}\)=\(\widehat{CMD}\)(vì đối đỉnh)
=>\(\widehat{CMD}\)=60 độ
xét t.giác MCD có: \(\widehat{CMD}\)+\(\widehat{MDC}\)+\(\widehat{MCD}\)=180 độ
=>60 độ+ 90 độ+ \(\widehat{MCD}\)=180 độ
=>\(\widehat{MCD}\)=30 độ(1)
Mặt khác \(\Delta\)ABC có:\(\widehat{ABC}\)+\(\widehat{BAC}\)+\(\widehat{ACB}\)=180 độ
=>60 độ+90 độ+\(\widehat{ACB}\)=180 độ
=> \(\widehat{ACB}\)=30 độ(2)
từ (1) và (2) suy ra\(\widehat{BCA}\)=\(\widehat{ACD}\)
c,
20 tháng 3 2023
\(\text{#TNam}\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB=AC,` \(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABM` và Tam giác `ACM:`
`AB=AC (CMT)`
\(\widehat{B}=\widehat{C}\)
`MB=MC (g``t)`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`b,` Xét Tam giác `AMB` và Tam giác `CMD:`
`AM=MD (g``t)`
\(\widehat{AMB}=\widehat{CMD}\) `( \text {2 góc đối đỉnh})`
`MB = MC (g``t)`
`=> \text {Tam giác AMB = Tam giác CMD (c-g-c)}`
`->`\(\widehat{ABC}=\widehat{DCB}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong
`-> \text {AB // CD}`
`c,` Vì Tam giác `AMB =` Tam giác `CMD (b)`
`-> AB=CD (\text {2 cạnh tương ứng})`
Mà `AB = AC (a)`
`-> AC = CD`
Xét Tam giác `ACD: AC = CD`
`-> \text {Tam giác ACD cân tại C}`
10 tháng 1 2022
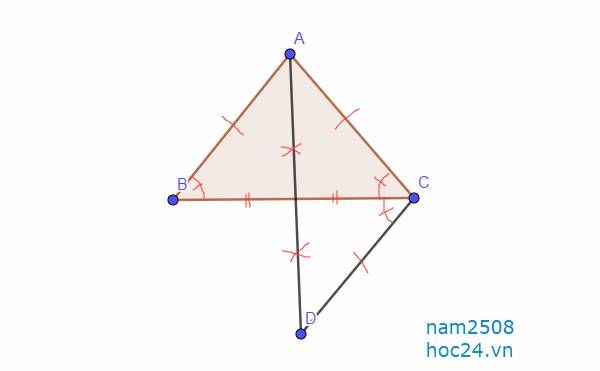
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AB//DC và AB=DC; \(\widehat{ACD}=90^0\)
b:
Ta có: ABDC là hình chữ nhật
nên AD=BC
XétΔBCA và ΔDAC có
BC=DA
CA chung
BA=DC
Do đó: ΔBCA=ΔDAC
Z
10 tháng 1 2022
a: Xét ΔAMB và ΔDMC có
MA=MD
MB=MC
Do đó: ΔAMB=ΔDMC
Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà
nên ABDC là hình chữ nhật
Suy ra: AB//DC và AB=DC;
b:
Ta có: ABDC là hình chữ nhật
nên AD=BC
XétΔBCA và ΔDAC có
BC=DA
CA chung
BA=DC
Do đó: ΔBCA=ΔDAC
Ta thấy: b + c > hoặc = 10
Xét cột hàng đơn vị và hàng chục ta có: b + c + 1= 10 + c
Suy ra: b = 9
Xét cột hàng trăm ta có: a + a + 1 = 9
Suy ra a = 4
Xét cột hàng đơn vị ta có: c + 9 = 4 (vô lý)
Suy ra c + 9 = 14.
Vậy c = 5 Phép cộng trên sẽ là: 495 + 459 = 954
bạn ghi sai đề rồi
sửa lại đề abc + acb = bca
giải
) abc + acb = bca
Ta có :
=>abc + acb =bca
=>c+b=a
=>b+c+1=c
Nên a+1=c
=>abc + acb = bca.
=>a00+bc +a00+cd = bca
=>2.a00+ bc+cb=b00 + c0 +a
=>a.100.2+b.10+c+c.10+b =b.100+c.10+a
=>a.200+11.(b+c)=b.100+c.10+a
=>a.200+11.1a=b.100+c.10+a
=>a.200+11.10+11.a=b.10.10+c.10+a
=>a.211+110=10.(b0+c)+a
=>a.21.10+11.10=10(b.10+c)
=>10.(a.21+11)=10(b.10+c)
=>a.21+11=b.10+c
=>a.21+11=b.10+c
Đoạn sau bạn tự giải nhé
Đáp án là 459 + 495 = 954