Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Số nguyên a là số hữu tỉ vì ta có thể viết a = \(\frac{a}{1}\)
3. Với a, b ∈ Z, b # 0
- Khi a, b cùng dấu thì a/b > 0
- Khi a, b khác dấu thì a/b < 0
Kết luận: Số hữu tỉ a/b (a, b ∈ Z, b # 0) dương nếu a, b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0.
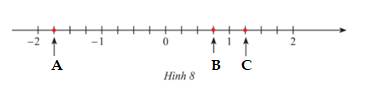
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:
?
a: \(-\dfrac{15}{20};\dfrac{24}{-32};-\dfrac{27}{36}\)
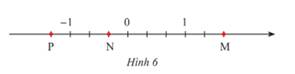
a) Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:\(\frac{5}{3};\,\frac{{ - 1}}{3};\,\frac{{ - 4}}{3}\).
b)
. B. 
. C. 
. D.
và 
. B. 
và 
và 
. D. 
và 
.
mà 
là:
. B. 
.
. D. 
là một số hữu tỉ. D. Số 0 là một số hữu tỉ dương.
.
. B. 
.
. D. 
.
a) Ta có: \( - 0,625 = \frac{{ - 625}}{{1000}}= \frac{{ - 625:125}}{{1000:125}} = \frac{{ - 5}}{8}\)
\(\begin{array}{l}\frac{5}{{ - 8}} = \frac{{ - 5}}{8};\\\frac{{10}}{{16}} = \frac{{10:2}}{{16:2}} = \frac{5}{8};\\\frac{{20}}{{ - 32}} = \frac{{20:( - 4)}}{{( - 32):( - 4)}} = \frac{{ - 5}}{8};\\\frac{{ - 10}}{{16}} = \frac{{( - 10):2}}{{16:2}} = \frac{{ - 5}}{8};\\\frac{{ - 25}}{{40}} = \frac{{( - 25):5}}{{40:5}} = \frac{{ - 5}}{8};\\\frac{{35}}{{ - 48}}\end{array}\)
Vậy các phân số biểu diễn số hữu tỉ -0,625 là:
\(\frac{5}{{ - 8}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}}\)
b) Ta có: \( - 0,625 = \frac{{ -5}}{{8}}\) nên ta biểu diễn số hữu tỉ \(\frac{{ -5}}{{8}}\) trên trục số.
Chia đoạn thẳng đơn vị thành 8 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{8}\) đơn vị cũ.
Lấy một điểm nằm trước O và cách O một đoạn bằng 5 đơn vị mới. Điểm đó biểu diễn số hữu tỉ \(\frac{{ -5}}{{8}}\)
Ta có : Vậy các phân số
cùng biểu diễn một số hữu tỉ
Tương tự cùng biểu diễn một số hữu tỉ
b) Ba phân số cùng biểu diễn số hữu tỉ là:
Ta có : Vậy các phân số
cùng biểu diễn một số hữu tỉ
Tương tự cùng biểu diễn một số hữu tỉ
b) Ba phân số cùng biểu diễn số hữu tỉ là:
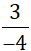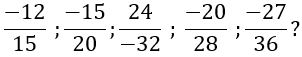
\(\frac{a}{\frac{b}{a,b}}=\frac{a}{\frac{b}{\frac{10a+b}{10}}}=\frac{a}{b}.\frac{10}{10a+b}=\frac{10a}{10ab+b^2}\)