Cho tam giác ABC vuông tại A,\. Vẽ đường cao AH. Trên BC lấy D sao cho BD=BA
a, CM góc BAD=góc ADB
b, CM AD là phân giác của góc HAC
c, vẽ DK vuông góc AC tại K. CM AK=AH
Mọi người giúp mình vs ạ. Cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 5 2022
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
YP
11 tháng 5 2022
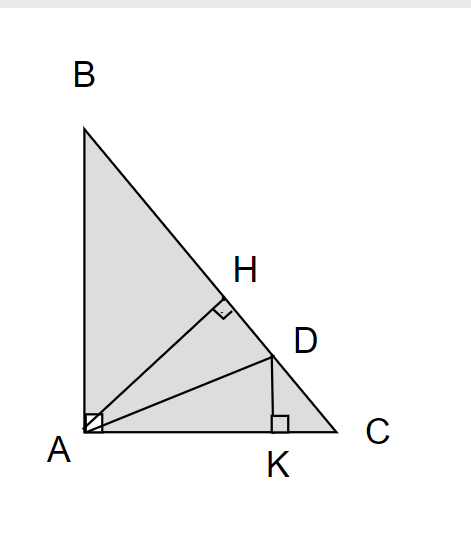
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)
26 tháng 3 2018
a,: Vì tam giac BAD có BA=BD=>BAD cân tại A
=>góc BAD=góc ADB( 2 cạnh đáy tam giác cân)
b,:Vì góc BAD=góc BDA(Cm câu a),Mà BAD+DAC=900(A vuong)
=>BDA+DAC=900MÀ BDA+HAD=900(2 góc nhon trong tam giac vg thi fu nhau)
=>HAD=DAC
=>AD la dug phân giác góc HAC
Câu c,d tu lam nhe, mik mỏi tay
2 tháng 5 2017
a, ta co AB = DB suy ra tam giac BAD can tai B (1)
từ (1) => góc BAD = góc ADB (DPCM)
TN
22 tháng 4 2016
a) Xét tam giac BAD ta có : BA=BD (gt)=> tam giac BAD cân tại B => goc BAD= góc ADB
b) ta có
goc BAD + goc DAK =90 ( 2 góc kề phụ )
goc ADB + goc HAD =90 ( tamg iac AHD vuông tại H)
goc BAD = goc ADB ( cm câu a)
==> goc DAK = goc HAD
==> AD là phân giác góc HAC
c)Xét tam giac AHD vuông tại H và tam giac AKD vuông tại K ta có
AD=AD ( cạnh chung)
goc HAD = goc DAK ( AD la phân giác góc HAC)
--> tam giác AHD = tam giác AKD ( ch - gn )
--> AH= AK ( 2 cạnh tương ứng )
d) ta có ;
AB < BH + AH ( bất đẳng thức trong tam giac ABH )
AC < HC + AH ( bất đẳng thức trong tam giac AHC )
--> AB+AC < BH +AH + HC+ AH
--> AB + AC < BC + 2 AH
( chúc bạn thi tốt )
3 tháng 8 2023
a) Ta có bd = ba (do đường cao ah là đường cao của tam giác vuông abc), và bd = ba nên tam giác abd là tam giác cân tại b.
Do đó, ad là đường phân giác của góc hacb (do ad là đường phân giác của tam giác abd).
b) Vẽ dk vuông góc với ac tại k. Ta cần chứng minh ak = ah.
Ta có tam giác akd vuông tại k, và tam giác ahd vuông tại h.
Do đó, ta cần chứng minh tam giác akd đồng dạng với tam giác ahd.
Ta có:
- Góc akd = góc ahd (vuông góc với ac)
- Góc kda = góc hda (cùng là góc nhọn)
- Cạnh ad chung
Do đó, tam giác akd đồng dạng với tam giác ahd.
Vậy, ak = ah.
c) Ta cần chứng minh ab + ac < bc + ah.
Ta có:
ab + ac = ab + ad + dc (do ad là tia phân giác của góc hacb)
= ab + ak + kc (do ak = ah và dk vuông góc với ac)
= ab + ah + kc (do ak = ah)
= ab + ah + hc (do kc = hc)
= ab + ah + bc (do ah là đường cao của tam giác abc)
= bc + ah + ab
= bc + ah + ba (do ab = ba)
= bc + ah.
Vậy, ab + ac < bc + ah.