Cho a/b = b/c. Chứng minh rằng nếu a/b = b/c thì a2 + b2/b2 + c2 = a/c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{a}{b}=\dfrac{b}{c}\Rightarrow ac=b^2\)
\(\dfrac{a^2+b^2}{b^2+c^2}=\dfrac{a^2+ac}{ac+c^2}=\dfrac{a\left(a+c\right)}{c\left(a+c\right)}=\dfrac{a}{c}\)


Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)

\(a,\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow\dfrac{a^2}{c^2}=\dfrac{c^2}{b^2}=\dfrac{a^2+c^2}{b^2+c^2}\left(1\right)\)
Mà \(\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow ab=c^2\Leftrightarrow\dfrac{a}{b}=\dfrac{c^2}{b^2}\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\tođpcm\)
\(b,\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow ab=c^2\)
\(\Leftrightarrow\dfrac{b^2-a^2}{a^2+c^2}=\dfrac{\left(b-a\right)\left(b+a\right)}{a^2+ab}=\dfrac{\left(b-a\right)\left(b+a\right)}{a\left(a+b\right)}=\dfrac{b-a}{a}\left(đpcm\right)\)

Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
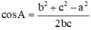
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.

Ta biến đổi : a2 ( b - c ) + b2 ( c - a ) + c2 ( a - b ) = 0 thành ( a - b ) ( b - c ) ( a - c ) = 0
Ta suy ra : a = b hoặc b = c hoặc c = a
Vậy 3 số a,b,c tồn tại 2 số bằng nhau
à quên, cách biến đổi như vậy bạn tham khảo ở đây : Câu hỏi của Tên của bạn - Toán lớp 8 - Học toán với OnlineMath
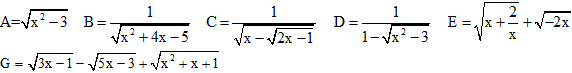 Mn giúp em với ;-;
Mn giúp em với ;-;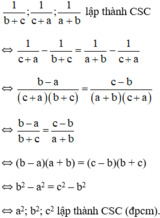
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{x}{5}=\frac{y}{7}=\frac{z}{9}=\frac{x-y+z}{5-7+9}=\frac{315}{7}=45\)
suy ra: x/5 = 45 => x = 225
y/7 = 45 => y = 315
z/9 = 45 => z = 405
Có \(\frac{a}{b}=\frac{b}{c}\Leftrightarrow\frac{a}{c}=\frac{b}{d}\)
Đặt \(\frac{a}{c}=\frac{b}{d}=k\Rightarrow a=c.k;b=d.k\)
\(\Rightarrow a^2=c^2.k^2;b^2=d^2.k^2\)
Khi đó \(\frac{a^2+c^2}{b^2+d^2}=\frac{c^2.k^2+c^2}{d^2.k^2+d^2}=\frac{c^2.\left(k^2+1\right)}{d^2.\left(k^2+1\right)}=\frac{c^2}{d^2}=\frac{a^2}{b^2}\)