Cho 3 điểm O(0;0), A(0;2), C(5;0).
a) Tìm tọa độ đỉnh B của hình chữ nhật OABC
b) Viết phương trình các đường thẳng chứa cạnh của hình chữ nhật
c) Viết phương trình các đường thẳng chứa đường chéo của hình chữ nhật
Ai đó giúp vớiiiiiiiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 7 2017
Các điểm nằm trên trục hoành là các điểm có tung độ bằng 0. Trong số các điểm ở trên ta thấy những điểm có tung độ bằng 0 là: A(-1; 0), D(3; 0), O(0; 0) . Vậy có ba điểm nằm trên trục hoành
Chọn đáp án D
CM
10 tháng 4 2019
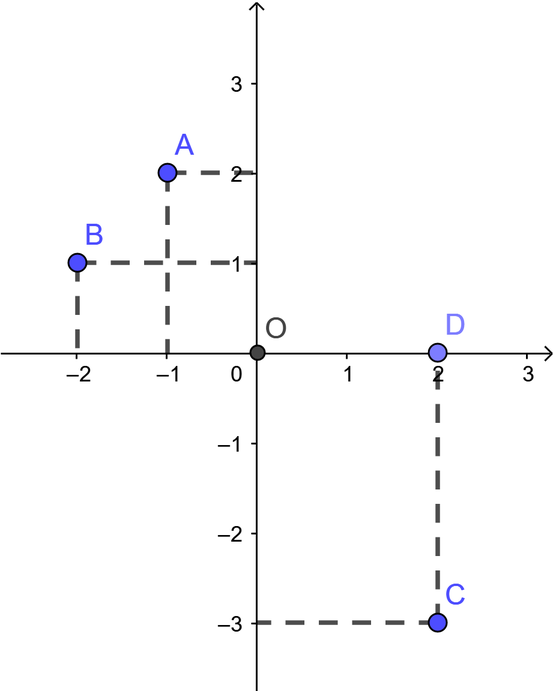
Biểu diễn các điểm trên hệ trục tọa độ Oxy ta thấy có hai điểm nằm trong góc phần tư thứ hai là A và B
Chọn đáp án C
XO
23 tháng 2 2023
a) A(3;-5) ; B(1;0)
=> \(\overrightarrow{AB}\left(-2;5\right)\)
Gọi C(x;y) tọa độ cần tìm
khi đó \(\overrightarrow{OC}\left(x;y\right)\)
\(\overrightarrow{OC}=-3\overrightarrow{AB}\Leftrightarrow\left\{{}\begin{matrix}x=-3.\left(-2\right)=6\\y=-3.5=-15\end{matrix}\right.\)
Vậy C(6;-15)
b) D đối xứng với A qua C
=> C trung điểm AD
Gọi D(x1;y1)
Ta có : \(6=\dfrac{3+x_1}{2}\Leftrightarrow x_1=9\)
\(-15=\dfrac{-5+y_1}{2}\) <=> y1 = -25
Vậy D(9;-25)
11 tháng 5 2022
a: Vì OA và OB là hai tia đối nhau
và OA=OB
nên O là trung điểm của AB
b: Để C là trung điểm của OB thì OC=1/2OB
hay a=1,5(cm)
CM
27 tháng 9 2019
Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = 3 x ta được:
+) Với M (1; 1), thay x = 1 ; y = 1 ta được 1 = 3 . 1 ⇔ 1 = 3 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = 3 . 0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (−1; −3), thay x = − 1 ; y = − 3 ta được − 3 = 3 . ( − 1 ) ⇔ − 3 = − 3 (luôn đúng) nên P ∈ (C)
+) Với Q (3; 9), thay x = 3 ; y = 9 ta được 9 = 3 . 3 ⇔ 9 = 9 (luôn đúng) nên Q ∈ (C)
+) Với M (−2; 6), thay x = − 2 ; y = 6 ta được 6 = 3 . ( − 2 ) ⇔ 6 = − 6 (vô lý) nên A (C)
Vậy có ba điểm thuộc đồ thị (C) trong số các điểm đã cho.
Đáp án cần chọn là: B
CM
21 tháng 4 2018
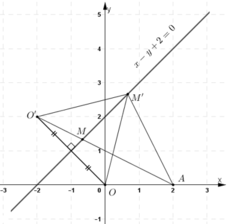
a, Cách 1: Gọi O’ là điểm đối xứng với O qua (Δ)
⇒ OO’ ⊥ Δ tại trung điểm I của OO’.
+ (Δ) nhận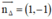 
là một vtpt ⇒ (Δ) nhận 
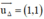là một vtcp
OO’ ⊥ Δ ⇒ OO’ nhận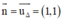 
là một vtpt. Mà O(0, 0) ∈ OO’
⇒ Phương trình đường thẳng OO’: x + y = 0.
+ I là giao OO’ và Δ nên tọa độ của I là nghiệm của hệ phương trình:
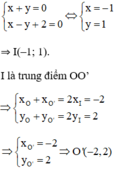
Cách 2: Gọi O’(x, y) là điểm đối xứng với O qua Δ.
+ Trung điểm I của OO’ là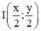 
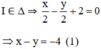
+ (Δ) nhận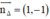 
là một vtpt ⇒ (Δ) nhận 
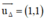là một vtcp.
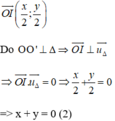
Từ (1) và (2) ta có hệ phương trình
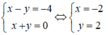
Vậy O’(–2; 2).
b)
+ Vì O và A nằm cùng một nửa mặt phẳng bờ là đường thẳng Δ nên đoạn thẳng OA không cắt Δ.
O’ và A thuộc hai nửa mặt phẳng khác nhau bờ là đường thẳng Δ nên O’A cắt Δ.
Do O’ đối xứng với O qua đường thẳng ∆ nên ∆ là đường trung trực của đoạn thẳng OO’, với mọi M ∈ Δ ta có MO = MO’.
Độ dài đường gấp khúc OMA bằng OM + MA = O’M + MA ≥ O’A.
⇒ O’M + MA ngắn nhất khi O’M + MA = O’A ⇔ M là giao điểm của O’A và Δ.
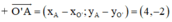
⇒ O’A nhận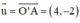 
là một vtcp
⇒ O’A nhận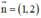 
là một vtpt. Mà A(2; 0) ∈ O’A
⇒ Phương trình đường thẳng O’A : 1(x - 2) + 2(y - 0)= 0 hay x + 2y – 2 = 0.
M là giao điểm của O’A và Δ nên tọa độ điểm M là nghiệm của hệ :
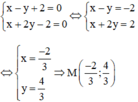
Vậy điểm M cần tìm là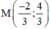 
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) \(\overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0 \)
\(\begin{array}{l}
\overrightarrow {OA} + 3\overrightarrow {OB} = \vec 0\\
\Leftrightarrow \overrightarrow {OB} + \overrightarrow {BA} + 3\overrightarrow {OB} = \vec 0\\
\Leftrightarrow \overrightarrow {OB} + 3\overrightarrow {OB} = - \overrightarrow {BA} \\
\Leftrightarrow 4\overrightarrow {OB} = \overrightarrow {AB} \\
\Leftrightarrow \overrightarrow {OB} = \frac{1}{4}\overrightarrow {AB}
\end{array}\)
Vậy O thuộc đoạn AB sao cho \(OB = \frac{1}{4}AB\)
b) Ta có:
\(\begin{array}{l}
\overrightarrow {MA} + 3\overrightarrow {MB} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\\
= \left( {\overrightarrow {MO} + 3\overrightarrow {MO} } \right) + \left( {\overrightarrow {OA} + 3\overrightarrow {OB} } \right)\\
= 4\overrightarrow {MO} + \overrightarrow 0 = 4\overrightarrow {MO} . (đpcm)
\end{array}\)
Đường thẳng đi qua A và B có dạng
\(y=ax+b\)
Mà \(A\left(0;2\right)\)
\(\Rightarrow y=2\)
Đường thẳng đi qua B và C cũng có dạng
\(y=ax+b\)
\(Mà\text{ }C\left(5;0\right)\)
\(\Rightarrow x=5\)
\(\Rightarrow B\left(5;2\right)\)
b) Đường thẳng đi qua \(OA\) là: \(y=0\)
Đường thẳng đi qua \(OC\) là \(x=0\)
Đường thẳng đi qua \(AB\) là \(y=2\)
Đường thẳng đi qua \(BC\) là \(x=5\)
c) Đường thẳng đi qua \(O\left(0;0\right);B\left(5;2\right)\) là
\(\dfrac{y-2}{0-2}=\dfrac{x-5}{0-5}\\ \Rightarrow\dfrac{2-y}{2}=\dfrac{5-x}{5}\\ \Rightarrow5\left(2-y\right)=2\left(5-x\right)\\ \Rightarrow10-5y=10-2x\\ \Rightarrow5y=2x\\ \Rightarrow y=\dfrac{2}{5}x\)
Đường thẳng đi qua \(A\left(0;2\right);C\left(5;0\right)\)là:
\(\dfrac{y-0}{2-0}=\dfrac{x-5}{0-5}\\ \Rightarrow\dfrac{y}{2}=\dfrac{5-x}{5}\\ \Rightarrow\dfrac{y}{2}=2-\dfrac{2}{5}x\)
bài này mà của lớp 9 sao bn