Cho \(0^o< \alpha< 90^o\) và \(\sin\alpha+\cos\alpha=\frac{7}{5}\). Tính \(\tan\alpha\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mn trả lời nhanh nhanh giùm em với ạ. Em đang cần gấp...
- Ta có: \(\sin\alpha+\cos\alpha=\frac{7}{5}\)
\(\Rightarrow\sin\alpha=\frac{7}{5}-\cos\alpha\)
- Theo tỉ số lượng giác của óc nhọn, ta có:
\(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\left(\frac{7}{5}-\cos\alpha\right)^2+\cos^2\alpha=1\)
\(\Leftrightarrow\frac{49}{25}-\frac{14}{5}\cos\alpha+\cos^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow50\cos^2\alpha-70\cos\alpha+48=0\)
\(\Leftrightarrow25\cos^2\alpha-35\cos\alpha+24=0\)
\(\Leftrightarrow\left(5\cos\alpha-4\right)\left(5\cos\alpha-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}5\cos\alpha-4=0\\5\cos\alpha-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\cos\alpha=\frac{4}{5}\\\cos\alpha=\frac{3}{5}\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}\sin\alpha=\frac{7}{5}-\cos\alpha=\frac{7}{5}-\frac{4}{5}=\frac{3}{5}\\\sin\alpha=\frac{7}{5}-\cos\alpha=\frac{7}{5}-\frac{3}{5}=\frac{4}{5}\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\frac{3}{5}}{\frac{4}{5}}=\frac{3}{4}\\\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{3}\end{cases}}\)
Kết luận: Vậy..........

( sin a + cos a )^2 = (7/5)^2
=> sin^2 a + cos^2a + 2.sina . cos a = 49/25
=> 1 + 2.sin a . cos a = 49/25
=> 2.sin a + cos a = 49/25 - 1 = 24 / 25
( sin a - cos a )^2 = sin ^2 a + cos ^2a - 2. sin a . cos a = 1 - 24/25 = 1/25
=> sin a - cos a = 1/5 (2)
TA có sina + cos a = 7/5 (1)
Từ (1) và (1) => 2 sina = 8/5 => sin a = 8/5 : 2 = 8/10 = 4/5
=> cos a = sin a - 1/5 = 4/5 - 1/5 = 3/5
tan a = \(\frac{sina}{cosa}=\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{5}\cdot\frac{5}{3}=\frac{4}{3}\)

a, ta có \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}\)
\(\frac{1}{3}\)= \(\frac{\sin\alpha}{\cos\alpha}\)
\(\cos\alpha\)= 3 \(\sin\alpha\)
ta có \(\frac{\cos\alpha+\sin\alpha}{\cos\alpha-\sin\alpha}\)= \(\frac{3\sin\alpha+\sin\alpha}{3\sin\alpha-\sin\alpha}\)= \(\frac{4\sin\alpha}{2\sin\alpha}\)= \(2\)
#mã mã#

a) Ta có A=\dfrac{\tan \alpha+3 \dfrac{1}{\tan \alpha}}{\tan \alpha+\dfrac{1}{\tan \alpha}}=\dfrac{\tan ^{2} \alpha+3}{\tan ^{2} \alpha+1}=\dfrac{\dfrac{1}{\cos ^{2} \alpha}+2}{\dfrac{1}{\cos ^{2} \alpha}}=1+2 \cos ^{2} \alphaA=tanα+tanα1tanα+3tanα1=tan2α+1tan2α+3=cos2α1cos2α1+2=1+2cos2α Suy ra A=1+2 \cdot \dfrac{9}{16}=\dfrac{17}{8}A=1+2⋅169=817.
b) B=\dfrac{\dfrac{\sin \alpha}{\cos ^{3} \alpha}-\dfrac{\cos \alpha}{\cos ^{3} \alpha}}{\dfrac{\sin ^{3} \alpha}{\cos ^{3} \alpha}+\dfrac{3 \cos ^{3} \alpha}{\cos ^{3} \alpha}+\dfrac{2 \sin \alpha}{\cos ^{3} \alpha}}=\dfrac{\tan \alpha\left(\tan ^{2} \alpha+1\right)-\left(\tan ^{2} \alpha+1\right)}{\tan ^{3} \alpha+3+2 \tan \alpha\left(\tan ^{2} \alpha+1\right)}B=cos3αsin3α+

Do \(90< a< 180\Rightarrow cosa< 0\Rightarrow tana< 0\Rightarrow\) đề bài sai do tana không thể bằng 3
Nhưng kệ cứ tính thì:
Chia cả tử và mẫu của A cho \(cos^3a\) và lưu ý \(\frac{1}{cos^2a}=1+tan^2a\)
\(A=\frac{tana.\frac{1}{cos^2a}+tan^2a+1}{tan^3a-tana-1}=\frac{tana\left(1+tan^2a\right)+tan^2a+1}{tan^3a-tana-1}\)
Tới đây thay số vào và bấm máy là xong

Tham khảo:
a)
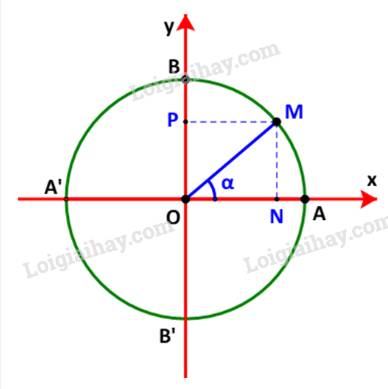
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha = {x^2}\\{\sin ^2}\alpha = {y^2}\end{array} \right.\)(1)
Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)
Từ (1) và (2) suy ra \({\sin ^2}\alpha + {\cos ^2}\alpha = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)
\( \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (vì OM =1). (đpcm)
b)
Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\)
\( \Rightarrow 1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)
c)
Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha < {180^o})\)
\( \Rightarrow 1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)
\(\sin^2\alpha+\cos^2\alpha=1\)
\(\Rightarrow\sin^2\alpha+\left(\frac{7}{5}-\sin\alpha\right)^2=1\)
\(\Rightarrow25\sin^2\alpha-35\sin\alpha+12=0\)
\(\Rightarrow\left(5\sin\alpha-4\right)\left(5\sin\alpha-3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}\sin\alpha=\frac{4}{5}\\\sin\alpha=\frac{3}{5}\end{cases}}\)
Nếu \(\sin\alpha=\frac{4}{5}\)thì \(\cos\alpha=\frac{3}{5}\Rightarrow\tan\alpha=\frac{4}{3}\)
Nếu \(\sin\alpha=\frac{3}{5}\)thì \(\cos\alpha=\frac{4}{5}\Rightarrow\tan\alpha=\frac{3}{4}\)
Tk cho mk bạn nhá