cho hình bình hành ABCD.gọi E là trung điểm của AD, F là trung điểm của BC. a chứng minh tứ giác EBDF là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
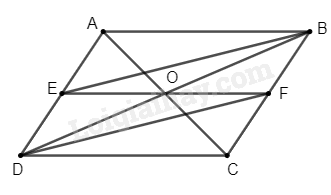
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng
27 tháng 10 2021
b: Xét tứ giác EBFD có
ED//BF
ED=BF
Do đó: EBFD là hình bình hành
MA
1 tháng 11 2021
tham khảo
a) Ta có: (F là trung điểm của AD)
(E là trung điểm của BC)
mà AD=BC(Hai cạnh đối trong hình bình hành ABCD)
nên AF=BE
Xét tứ giác AFEB có
AF//BE(AD//BC, F∈AD, E∈BC)
AF=BE(cmt)
Do đó: AFEB là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Ta có: (gt)
mà (F là trung điểm của AD)
nên AB=AF
Hình bình hành AFEB có AB=AF(cmt)
nên AFEB là hình thoi(Dấu hiệu nhận biết hình thoi)
⇒Hai đường chéo AE và BF vuông góc với nhau tại trung điểm của mỗi đường(Định lí hình thoi)
hay AE⊥BF(đpcm)
b) Ta có: AFEB là hình thoi(cmt)
nên AF=FE=EB=AB và (Số đo của các cạnh và các góc trong hình thoi AFEB)
hay
Xét ΔFEB có FE=EB(cmt)
nen ΔFEB cân tại E(Định nghĩa tam giác cân)
Xét ΔFEB cân tại E có (cmt)
nên ΔFEB đều(Dấu hiệu nhận biết tam giác cân)
⇒(Số đo của một góc trong ΔFEB đều)
Ta có: AB//FE(hai cạnh đối trong hình thoi ABEF)
nên (hai góc đồng vị)
hay
Ta có: tia FE nằm giữa hai tia FB,FD
nên
(1)
Ta có: AD//BC(hai cạnh đối trong hình bình hành ABCD)
nên (hai góc trong cùng phía bù nhau)
hay (2)
Từ (1) và (2) suy ra
Xét tứ giác BFDC có
FD//BC(AD//BC, F∈AD)
nên BFDC là hình thang có hai đáy là FD và BC(Định nghĩa hình thang)
Hình thang BFDC có (cmt)
nên BFDC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
22 tháng 7 2015
Vì ABCD là HBH => AD = BC (1)
CM = 1/2 BC ( M là tđ) (2)
AN = 1/2 AD ( N là tđ) (3)
Tuwf (1) (2) vaf (3) => AN = CM
tg AMCN cos AN =CM
AN // CM( AD // BC)
=> AMCN là HBH
b, HT ABCD có AN = ND
BM = MC
=> MN là đg tb => MN // AB // BC (4)
ABCD là HBH => OB = OD ; OA = OC ( tính chất HBH)
Tam giác AOD có AN = ND
OB = OD
=> ON là đg tb => ON //AB (5)
CMTT T OM //DC (6)
Từ(4) (5) và (6) => N , O , M thẳng hàng
15 tháng 11 2021
5. Vì tứ giác ABCD là hình bình hành (gt)
=> AD // BC ; AD = BC (tc)
Vì M là trung điểm AD (gt)
N là trung điểm BC (gt)
AD = BC (cmt)
=> AM = DM = BN = CN
Vì AD // BC mà M ∈ AD, N ∈ BC
=> MD // BN
Xét tứ giác MBND có : MD = BN (cmt)
MD // BN (cmt)
=> Tứ giác MBND là hình bình hành (DHNB)
=> BM = DN (tc hình bình hành)
15 tháng 11 2021
6. Vì tứ giác ABCD là hình bình hành (gt)
=> AB // CD ; AB = CD (tc)
Vì E là trung điểm AB (gt)
F là trung điểm CD (gt)
AB = CD (cmt)
=> AE = BE = DF = DF
Vì AB // CD mà E ∈ AB, F ∈ CD
=> BE // DF
Xét tứ giác DEBF có : BE = DF (cmt)
BE // DF (cmt)
=> Tứ giác DEBF là hình bình hành (DHNB)
a) E là trung điểm của AD
F là trung điểm của BC
mà AD = BC (ABCD là hình bình hành)
nên AE = CF
Xét tam giác ABE và tam giác CDF có
góc A = góc C (ABCD là hình bình hành)
AB = CD (ABCD là hình bình hành)
AE = CF (cmt)
Suy ra tam giác ABE = tam giác ACF (cgc)
\(\Rightarrow\) góc E1 = góc F1
mà góc D1 = góc F1 (AD//BC,ABCD là hình bình hành)
nên góc E1 = góc D1
mà 2 góc này có vị trí đồng vị nên EB // DF
Tứ giác EBFD có EB // DF (cmt)
ED // BF (AD // BC, ABCD là hình bình hành)
\(\Rightarrow\) EBFD là hình bình hành