Cho tam giác ABC có AC>AB . So sánh 2 góc ngoài tại đỉnh B và đỉnh C
GIÚP MK VS MAI MK CẦN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
L
25 tháng 2 2021
ta có vì AB < AC nên góc ABC lớn hơn góc ACB ( tính chất cạnh đối với góc lớn hơn là cạnh lớp hơn và ngược lại )
mà ABC kề bù với góc ngoài nên ABC + góc ngoài của góc ABC = 180 độ
ta có ACB kề bù với góc ngoài nên góc ACB + góc ngoài của góc ACB =180 độ
ta có góc ABC lớn hơn góc ACB nên góc ngoài của góc ABC nhỏ hơn góc ngoài của góc ACB ( đpcm )
14 tháng 3 2022
a: Xét ΔABC có AB>AC
nên \(\widehat{B}< \widehat{C}\)
b: Vì \(\widehat{B}< \widehat{C}\)
nên góc ngoài tại đỉnh B lớn hơn góc ngoài tại đỉnhC
CM
15 tháng 8 2019
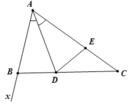
b. Giả sử góc ngoài tại đỉnh B của tam giác ABC là ∠(xBC). Ta có:
∠(xBC) + ∠(ABD) = 180o ⇒ ∠(xBC) = 180o - ∠(ABD) (0.5 điểm)
∠(DEC) + ∠(AED) = 180o ⇒ ∠(DEC) = 180o - ∠(AED) (0.5 điểm)
Mà ∠(ABD) = ∠(AED) ( hai góc tương ứng vì ΔABD = ΔAED)(0.5 điểm)
Từ đó suy ra ∠(xBC) = ∠(DEC) (0.5 điểm)
30 tháng 7 2018
a) Gọi số đo các góc A, góc B, góc C của tam giác ABC lần lượt là: a,b,c
ta có: a:b:c = 6:3:1
\(\Rightarrow\frac{a}{6}=\frac{b}{3}=\frac{c}{1}\)
- Tổng 3 góc trong tam giác ABC = 180 độ ( định lí)
=> a + b + c = 180 độ
ADTCDTSBN
có: \(\frac{a}{6}=\frac{b}{3}=\frac{c}{1}=\frac{a+b+c}{6+3+1}=\frac{180}{10}=18\)
=> a/6 = 18 => a = 108
b/3 = 18 => b = 54
c/1 = 18 => c = 18
KL:...
b)
Xét tam giác ABC
có: góc ACx = góc A 1 + góc B ( tính chất góc ngoài)
thay số: góc ACx = 108 độ + 54 độ
góc ACx = 162 độ
mà góc C1 =góc ACx/2 = 162 độ/2 = 81 độ
=> góc C1 = 81 độ
Lại có: góc A2 = góc B + góc C3 ( tính chất góc ngoài)
thay số: góc A2 = 54 độ + 18 độ
góc A2 = 72 độ
Xét tam giác AMC
có: góc AMC + góc C1 + góc A2 = 180 độ ( tổng 3 góc trong tam giác)
thay số: góc AMC + 81 độ + 72 độ = 180 độ
góc AMC = 180 độ - 81 độ - 72 độ
góc AMC = 27 độ
NV
1
19 tháng 2 2022
\(AC>AB\Rightarrow\widehat{B}>\widehat{C}\Rightarrow180^0-\widehat{B}< 180^0-\widehat{C}\Rightarrow\)Góc ngoài tại đỉnh B nhỏ hơn góc ngoài tại đỉnh C
PT
1
21 tháng 3 2018
ta có tam giác abc cân tại a có số đo là 100 độ
=> B =C = (180-100)/2 = 40 độ
vì hai đường phân giác của hai góc B và C trong tam giác abc cắt nhau tại i
=> CBI= BCI= 40/2 = 20 độ
vì tổng số đo các góc trong tam giác = 180 độ
=> BIC = 180 - CBI-BIC= 180 -(20+20) = 140 (độ)
Xét tam giác ABC có AC>AB
=>\(\widehat{ACB}\) >\(\widehat{ABC}\) (T/C góc và cạnh đối diện)
mà \(\widehat{ACB}\) + góc ngoài tại đỉnh C=180 độ
mà \(\widehat{ABC}\) + góc ngoài tại đỉnh B = 180 độ
=> Góc ngoài tại đỉnh C>góc ngoài tại đỉnh B