Cho tam giác ABC có góc B=70 độ, góc C=30 độ. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H thuộc BC).
a) Tính góc BAC
b) Tính góc ADH
c) Tính góc HAD
#Ai giải nhah bài này mình tick kb cho nèk
#Có vẽ hình nữa nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 11 2023
a: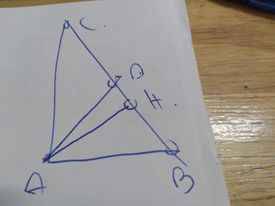 
b: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot90^0=45^0\)
Xét ΔADC có \(\widehat{ADH}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADH}=\widehat{DAC}+\widehat{DCA}\)
=>\(\widehat{ADH}=45^0+30^0=75^0\)
b: ΔHAD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HAD}+75^0=90^0\)
=>\(\widehat{HAD}=15^0\)
Vì \(\widehat{DAH}< \widehat{DAB}\)
nên AH nằm giữa AD và AB
=>\(\widehat{DAH}+\widehat{BAH}=\widehat{BAD}\)
=>\(\widehat{BAH}+15^0=45^0\)
=>\(\widehat{BAH}=30^0>\widehat{HAD}\)
d: \(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAC}+\widehat{C}=90^0\)(ΔAHC vuông tại H)
Do đó: \(\widehat{ABC}=\widehat{HAC}\)
26 tháng 11 2023
`a)`
`b)`
Có `Delta ABC` vuông tại `A` có `hat(C)=30^0`
`=>hat(B)=60^0`
`AD` là phân giác `hat(BAC)=>hat(BAD)=hat(A_3)=1/2hat(BAC)`
`=>hat(BAD)=hat(A_3)=1/2*90^0=45^0`
`Delta BAD` có `hat(B)+hat(D_1)+hat(BAD)=180^0`
hay `60^0+hat(D_1)+45^0=180^0`
`=>hat(D_1)=180^0-60^0-45^0=75^0`
`c)`
Có `Delta AHD` vuông tại `H(AH⊥BC)` có `hat(D_1)=75^0`
`=>hat(A_1)=15^0`
Có `hat(A_1)+hat(A_2)=hat(BAD)`
hay`15^0+hat(A_2)=45^0`
`=>hat(A_2)=30^0`
Có `15^0<30^0`
`=>hat(A_1)<hat(A_2)`
`d)`
Có `hat(A_1)+hat(A_3)=hat(HAC)`
hay `15^0+45^0=hat(HAC)`
`=>hat(HAC)=60^0`
Có `60^0=60^0`
`=>hat(B)=hat(HAC)`
16 tháng 7 2016
Ta có
góc A + góc B + góc C = 1800
=> góc a + 700 + 300 = 1800
=> góc A = 800
13 tháng 8 2021
a: Xét ΔADC có
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{ADH}=180^0-30^0-45^0\)
hay \(\widehat{ADH}=105^0\)
Vẽ đại đấy
a, \(\Delta ABC\)có: \(\widehat{BAC}+\widehat{BCA}+\widehat{CBA}=180^o\)(định lý tổng 3 góc trong tam giác)
hay \(\widehat{BAC}+30^o+70^o=180^o\)
\(\widehat{BAC}=70^o\)
b, Ta có: AD là phân giác của \(\widehat{BAC}\Rightarrow\widehat{BAD}=\widehat{DAC}=\frac{\widehat{BAC}}{2}=\frac{70^o}{2}=35^o\)
\(\Delta BAD\)có: \(\widehat{BAD}+\widehat{ADB}+\widehat{ABD}=180^o\)(định lý tổng 3 góc trong tam giác)
hay \(35^o+\widehat{ADB}+70^o=180^o\)
\(\widehat{ADB}=75^o\Leftrightarrow\widehat{ADH}=75^o\)
c, \(\Delta AHD\)có: \(\widehat{AHD}=90^o\Rightarrow\widehat{HAD}+\widehat{ADH}=90^o\)(2 góc nhọn phụ nhau)
hay \(\widehat{HAD}+75^o=90^o\Leftrightarrow\widehat{HAD}=15^o\)
;h;ilp9